题目内容
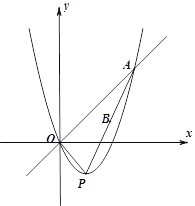
【题目】如图,已知直线![]() 与二次函数
与二次函数![]() 的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=
的图像交于点A、O,(O是坐标原点),点P为二次函数图像的顶点,OA=![]() ,AP的中点为B.
,AP的中点为B.
(1)求二次函数的解析式;
(2)求线段OB的长;
(3)若射线OB上存在点Q,使得△AOQ与△AOP相似,求点Q的坐标.
【答案】![]() ;(2)
;(2)![]() ; (3)点Q的坐标
; (3)点Q的坐标![]() 时,△AOQ与△AOP相似.
时,△AOQ与△AOP相似.
【解析】
(1)由点A在直线y=x上,可知A的横纵坐标相等,又因为OA=![]()
,所以可以求出A的坐标,再把O和A的坐标代入y=x2+bx+c,求出b和c的值即可求出函数的解析式;
(2)用配方法求出顶点P的坐标,再利用勾股定理求出OP的长和AP的长,利用勾股定理的逆定理即可判定三角形AOP的形状,进而求出OB的长;
(3)若△AOQ与△AOP相似,则①△AOP∽△OQA或②△AOP∽△OAQ,根据相似三角形的性质得到比例式,求出满足题意的OQ值即可.
(1)∵点A在直线![]() 上,且
上,且![]() ,∴A(3,3) .
,∴A(3,3) .
∵ 点O(0,0),A(3,3)在![]() 的图像上,
的图像上,
∴![]() ,解得:
,解得:![]() 。∴二次函数的解析式为
。∴二次函数的解析式为![]() .
.
(2)由题意得顶点P(1,-1)。∴![]()
∴![]() ,∴∠AOP=90°.
,∴∠AOP=90°.
∵∠AOP=90°,B为AP的中点 ,∴![]() .
.
(3) ∵∠AOP=90°,B为AP的中点 ,∴OB=AB .∴∠AOB=∠OAB.
若△AOQ与△AOP相似,,则①△AOP∽△OQA ,
∴![]() ,∴
,∴![]() .
.
②△AOP∽△OAQ ,∴![]()
![]() .
.
∵B(2,1) ∴![]() .
.
即点Q的坐标![]() 时,△AOQ与△AOP相似.
时,△AOQ与△AOP相似.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,小宇根据他们的成绩(单位:环)绘制了如下尚不完整的统计表:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | a | 6 |
乙成绩 | 7 | 5 | 7 | 4 | 7 |
(1)若甲成绩的平均数为6环,求a的值;
(2)若甲成绩的方差为3.6,请计算乙成绩的方差并说明谁的成绩更稳定?