题目内容
【题目】如图,A、B、C、P四点均在边长为1的小正方形网格格点上.
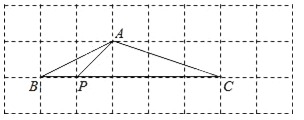
(1)判断△PBA与△ABC是否相似,并说明理由;
(2)求∠BAC的度数.
【答案】(1)相似;(2)135°.
【解析】试题分析:(1)△PBA与△ABC相似,利用勾股定理计算出AB的长,利用两边对应成比例且一个夹角对应相等的两个三角形相似可证明结论成立;
(2)由(1)可知:∠BAC=∠BPA,因为∠BPA易求,问题得解.
试题解析:解:(1)△PBA与△ABC相似.理由如下:
∵AB=![]() ,BC=5,BP=1,∴
,BC=5,BP=1,∴![]() .∵∠PBA=∠ABC,∴△PBA∽△ABC;
.∵∠PBA=∠ABC,∴△PBA∽△ABC;
(2)∵△PBA∽△ABC,∴∠BAC=∠BPA.∵∠BPA=90°+45°=135°,∴∠BAC=135°.

【题目】为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:
零花钱数额 | 人数(频数) | 频率 |
| 6 | 0.15 |
| 12 | 0.30 |
| 16 | 0.40 |
|
| 0.10 |
| 2 |
|

请根据以下图表,解答下列问题:
(1)这次被调查的人数共有__________人,![]() __________;
__________;
(2)计算并补全频数分布直方图;
(3)请估计该校1500名学生中每月零花钱数额低于90的人数.
【题目】为准备参加某市2019年度中小学生机器人竞赛,学校对甲、乙两支机器人制作小队所创作的机器人分别从创意、设计、编程与制作三方面进行量化,各项量化满分100分,根据量化结果择优推荐.它们三项量化得分如下表:
量化项目 | 量化得分 | |
甲队 | 乙队 | |
创意 | 85 | 72 |
设计 | 70 | 66 |
编程与制作 | 64 | 84 |
(1)如果根据三项量化的平均分择优推荐,哪队将被推荐参赛?
(2)根据本次中小学生机器人竞赛的主题要求,如果学校根据创意、设计、编程与制作三项量化得分按![]() 的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议.
的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议.