题目内容
【题目】已知,如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 为⊙
为⊙![]() 上一点,
上一点,![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的延长线上一点,且
的延长线上一点,且![]() .
.
(1)试判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若⊙![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.
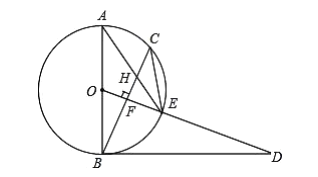
【答案】(1)见解析;(2)![]()
【解析】
(1)由∠ABC=∠AEC,![]() ,得
,得![]() ,进而得AB⊥BD,即可得到结论;
,进而得AB⊥BD,即可得到结论;
(2)连接BE,得∠AEB=90°,BE=6,易证BE~AEB,从而得![]() ,即可求解.
,即可求解.
(1)直线![]() 与⊙
与⊙![]() 相切,理由如下:
相切,理由如下:
∵∠ABC与∠AEC是同弧所对的圆周角,
∴∠ABC=∠AEC,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴∠ABC+∠BOD=∠ODB+∠BOD=90°,即:AB⊥BD,
∴直线![]() 是⊙
是⊙![]() 的切线;
的切线;
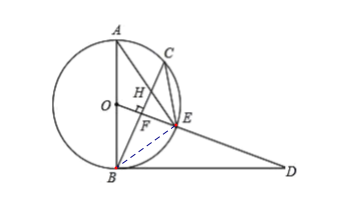
(2)连接BE,
∵AB是直径,
∴∠AEB=90°,
∵⊙![]() 的半径为
的半径为![]() ,
,![]() ,
,
∴BE=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴∠A=∠EBH,
又∵∠BEH=∠AEB,
∴BE~AEB,
∴![]() ,即:
,即:![]() ,解得:
,解得:![]() =
=![]() .
.

练习册系列答案
相关题目
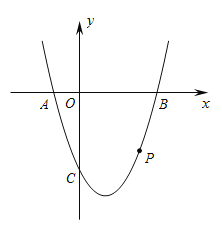
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()