Question

【题目】（教材呈现）

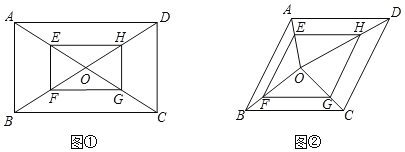
下图是华师版九年级上册数学教材第79页的部分内容．

请根据教材内容，结合图①，写出完整的解题过程．

（结论应用）

（1）在图①中，若AB=2，∠AOD=120°，则四边形EFGH的面积为______．

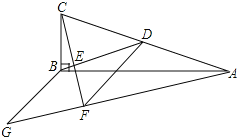
（2）如图②，在菱形ABCD中，∠BAD=120°，O是其内任意一点，连接O与菱形ABCD各顶点，四边形EFGH的顶点E、F、G、H分别在AO、BO、CO、DO上，EO=2AE，EF∥AB∥GH，且EF=GH，若△EFO与△GHO的面积和为，则菱形ABCD的周长为______．

Answer 1

【答案】 24．

【解析】

教材呈现：由矩形的性质得出OA=OB=OC=OD，再证出OE=OF=OG=OH，即可得出结论．

结论应用：（1）证明△OEF为等边三角形，得出∠EFO=60°，可求出EF=1，EH=，则答案可求出；

（2）过点G作GN⊥EF于点N，由条件可知四边形EFGH为平行四边形，可得∠EFG=60°，设EF=x，则NG=，由△EFO与△GHO的面积和为4列出方程求出x，证明△OEF∽△OAB，可得，可求出AB的长．则答案可求出．

解：教材呈现：

∵四边形ABCD是矩形，

∴OA=OC，OB=OD，AC=BD，

∴OA=OC=OB=OD．

∵AO，BO，CO，DO的中点E，F，G，H，

∴OE=OF=OG=OH，

∴四边形EFGH是矩形．

∵EG=FH，

∴四边形EFGH是矩形．

结论应用：

（1）∵AB=2，

∴EF=．

∵∠BAD=90°，

∴∠FEH=90°．

∵∠AOD=120°，

∴∠EOF=60°，

∴△OEF为等边三角形，

∴∠EFO=60°，

∴，

∴四边形EFGH的面积为1×．

故答案为：．

（2）过点G作GN⊥EF于点N，

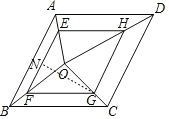
∵EF∥GH，且EF=GH，

∴四边形EFGH为平行四边形，

∴FG∥BC．

∵∠BAD=120°，

∴∠ABC=∠EFG=60°，

设EF=x，则NG=．

∵△EFO与△GHO的面积和为4，

∴，

解得：x=4，∴EF=4．

∵EF∥AB，∴△OEF∽△OAB，

∴．

∵EO=2AE，

∴，

∴AB=6，

∴菱形ABCD的周长为24．

故答案为：24．