题目内容
【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ. 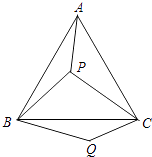
(1)观察并猜想AP与CQ之间的大小关系,并说明理由.
(2)若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由.
【答案】
(1)解:AP=CQ.理由如下:
∵∠PBQ=60°,且BQ=BP,
∴△BPQ为等边三角形,
∵∠ABP+∠CBP=60°,∠CBQ+∠CBP=60°,
∴∠CBQ=∠ABP,
在△ABP和△CBQ中,
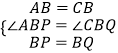 ,
,
∴△ABP≌△CBQ(SAS),
∴AP=CQ
(2)解:∵等边△ABC和等边△BPQ中,
PB=PQ=4,PA=QC=3,
∵PQ2+CQ2=PC2,
∴△PQC为直角三角形(勾股定理逆定理)
【解析】(1)易证△ABP≌△CBQ,可得AP=CQ;(2)根据PA=CQ,PB=BQ,即可判定△PQC为直角三角形.
【考点精析】解答此题的关键在于理解勾股定理的逆定理的相关知识,掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.

练习册系列答案
相关题目