题目内容
如图,点E(0,3),O(0,0),C(4,0)在⊙A上,BE是⊙A上的一条弦.则cos∠OBE= .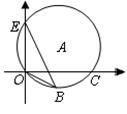


试题分析:连接EC,由90°的圆周角所对的弦为直径,根据∠EOC=90°得到EC为圆A的直径,所以点A在EC上且为EC中点,在直角三角形EOC中,由OE和OC的长,利用勾股定理求出EC的长,根据同弧所对的圆周角都相等得到∠EBO与∠ECO相等,而∠ECO在直角三角形EOC中,根据余弦函数定义即可求出cos∠ECO的值,进而得到cos∠EBO.
连接EC,

∵∠EOC=90°
∴BC为圆A的直径,
∴EC过点A,
又OE=3,OC=4,根据勾股定理得:EC=5,
∵∠OBE=∠OCE,
则cos∠OBE=cos∠OCE=
 .
.点评:解题的关键是熟练掌握90°的圆周角所对的弦为直径,同弧所对的圆周角相等,连接EC且得到EC为圆A的直径是解本题的突破点.

练习册系列答案
相关题目
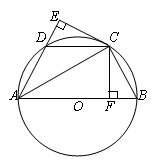
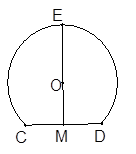
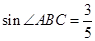 ,圆O经过点B、C,圆心O在△ABC的内部,且到点A的距离为2,求圆O的半径.
,圆O经过点B、C,圆心O在△ABC的内部,且到点A的距离为2,求圆O的半径.

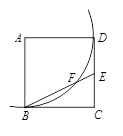
 ,求DE的长.
,求DE的长.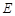 是正方形
是正方形 的边
的边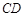 上一点,以
上一点,以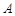 为圆心,
为圆心,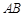 为半径的弧与
为半径的弧与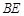 交于点
交于点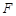 ,则
,则 .
.