题目内容
【题目】在平面直角坐标系![]() 中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
中,对于任意点P,给出如下定义:若⊙P的半径为1,则称⊙P为点P的“伴随圆”.
(1)已知,点![]() ,
,
①点![]() 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);
②点![]() 在点P的“伴随圆” (填“上”或“内”或“外”);
在点P的“伴随圆” (填“上”或“内”或“外”);
(2)若点P在![]() 轴上,且点P的“伴随圆”与直线
轴上,且点P的“伴随圆”与直线![]() 相切,求点P的坐标;
相切,求点P的坐标;
【答案】(1)上;外;(2)点P (2,0)或(2,0).
【解析】分析:(1)计算PA、PB的长,然后与半径1比较大小即可得出结论;
(2)连接PH,由点![]() 的“伴随圆”与直线
的“伴随圆”与直线![]() 相切,得到PH⊥OH,PH=1,∠POH=30°,则OP=2,由此即可得到结论.
相切,得到PH⊥OH,PH=1,∠POH=30°,则OP=2,由此即可得到结论.
详解:(1)①PA=![]() =1.
=1.
故选A在⊙P上.故答案为:上;
②PB=![]() =2>半径1,∴B在⊙P外.故答案为:外.
=2>半径1,∴B在⊙P外.故答案为:外.
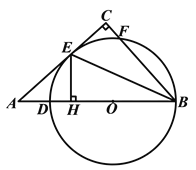
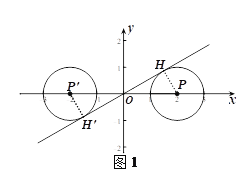
(2)连接![]() ,如图1.
,如图1.
∵点![]() 的“伴随圆”与直线
的“伴随圆”与直线![]() 相切,
相切,
∴PH⊥OH,
∴PH=1,∠POH=30°,
可得:OP=2,
∴点P(2,0)或(-2,0).

练习册系列答案
相关题目