题目内容
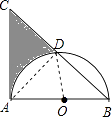
【题目】如图，等腰直角△ABC中，AB=AC=8，以AB为直径的半圆O交斜边BC于D，则阴影部分面积为（结果保留π）（ ）
A.24﹣4π
B.32﹣4π
C.32﹣8π
D.16
【答案】A
【解析】连接AD，OD，
∵等腰直角△ABC中，
∴∠ABD=45°．
∵AB是圆的直径，
∴∠ADB=90°，
∴△ABD也是等腰直角三角形，
∴ 
= 
．
∵AB=8，
∴AD=BD=4 
，
∴S阴影=S△ABC﹣S△ABD﹣S弓形AD=S△ABC﹣S△ABD﹣（S扇形AOD
﹣ 
S△ABD）= ×8×8﹣ ×4 ×4 ﹣ 
+ × ×4 ×4 =16﹣4π+8=24﹣4π．
故答案为：A．
连接AD，OD，依据阴影部分的面积=S△ABC﹣S△ABD﹣S弓形AD求解即可.
练习册系列答案
星级口算天天练系列答案
相关题目
