Question

【题目】在平面直角坐标系xOy中，反比例数y＝的图象过点A（6，1）．

（1）求反比例数的表达式；

（2）过点A的直线与反比例数y＝图象的另一个交点为B，与y轴交点交于点P．

①若点P为原点，直接写出点B的坐标；

②若PA＝2PB，求点P的坐标．

Answer 1

【答案】（1）y＝；（2）①B点的坐标为（﹣6，﹣1）；②P的坐标为（0，﹣1）．

【解析】

（1）由点A的坐标利用反比例函数图象上点的坐标特征即可求出m值，从而得出反比例函数表达式；

（2）①根据中心对称的性质即可求得；

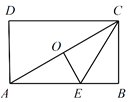
②作AC⊥y轴于C，BD⊥y轴于D，通过证得△APC∽△BPD，得出2，求得B的横坐标坐标，代入解析式求得坐标，然后根据待定系数法求得直线AB的解析式，令x=0，即可求得P的坐标．

（1）把（6，1）代入反比例函数解析式，得1，∴m=6；

（2）①由于直线过原点，该函数为正比例函数．

∵正比例函数和反比例函数图象都是关于原点中心对称的，∴两图象的交点关于原点成中心对称，∴点B、点A关于原点成中心对称．

∵A点的坐标为（6，1），∴B点的坐标为（﹣6，﹣1）．

②作AC⊥y轴于C，BD⊥y轴于D．

∵AC∥BD，∴△APC∽△BPD，∴．

∵AP=2PB，∴AC=2BD．

∵AC=6，∴BD=3，∴B的横坐标为﹣3，把x=﹣3代入y得y=﹣2，∴B（﹣3，﹣2），设直线AB的解析式为y=kx+b，把A（6，1），B（﹣3，﹣2）代入得，解得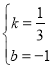：，∴直线AB的解析式为yx﹣1，令x=0，则y=﹣1，∴P的坐标为（0，﹣1）．