Question

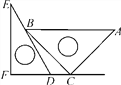
【题目】一副三角板如图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，∠E＝30°，∠A＝45°，AC＝12，试求CD的长．

Answer 1

【答案】CD＝12－4.

【解析】试题分析：过点B作BM⊥FD于点M，根据题意可求出BC的长度，然后在△EFD中可求出∠EDF=60°，求得MD的长，进而求得CD的长．

试题解析：

过点B作BM⊥FD于点M，

在△ACB中，∠ACB=90°，∠A=45°，AC=，

∴BC=AC=，∠ABC=45°，

∵AB∥CF，

∴∠BCM=∠ABC=45°，

∴BM＝BC·sin45°＝12，CM＝BM＝12，

∴在△EFD中，∠F=90°，∠E=30°，

∴∠EDF=60°.

∴MD=BM÷tan60°= ，

∴CD=CM－MD=12－.