题目内容
【题目】如图,在△ABC中,AB=AC,D是BC边的中点,点E,F分别在AD及其延长线上,且CE∥BF,连接BE,CF.
(1)求证:四边形EBFC是菱形;
(2)若BD=4,BE=5,求四边形EBFC的面积.

【答案】(1)见解析;(2)24.
【解析】
(1)由D是BC边的中点,CE∥BF,利用ASA易证得△BDF≌△CDE,即可得CE=BF,然后由一组对边平行且相等的四边形是平行四边形,证得四边形BFCE是平行四边形;
由AB=AC,D是BC边的中点,即可得AD⊥BC,又由四边形BFCE是平行四边形,根据对角线互相垂直的平行四边形是菱形,即可证得四边形BFCE是菱形.
(2)求出BC、EF即可解决问题;
(1)证明:∵D是BC边的中点,
∴BD=CD,
∵CE∥BF,
∴∠DBF=∠ECD,
在△BDF和△CDE中,
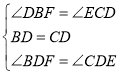 ,
,
∴△BDF≌△CDE(ASA),
∴CE=BF,
又∵CE∥BF,
∴四边形BFCE是平行四边形;
∵AB=AC,D是BC的中点,
∴AD⊥BC,
又∵四边形BFCE是平行四边形,
∴四边形BFCE是菱形.
(2)解:在Rt△BDE中,BE=5,BD=4,
∴DE=![]() =3,
=3,
∵四边形BECF是菱形,
∴EF=2DE=6,BC=2BD=8,
∴菱形BECF的面积=![]() ×6×8=24.
×6×8=24.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目