��Ŀ����
����Ŀ����OΪֱ��AB��һ�㣬����O������OC����һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����
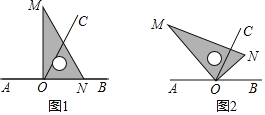
��1����ͼ1������BOC��65���������ǰ�MON��һ��ON������OB�غ�ʱ�����MOC���� ����
��2����ͼ2������BOC��65���������ǰ�MON�Ƶ�O��ʱ����תһ���Ƕȣ���ʱOC�ǡ�MOB�Ľ�ƽ���ߣ����BON���� ����
��3����ͼ2������BOC��������Ȼ�����ǰ�MON��ת��OCΪ��MOB�Ľ�ƽ���ߵ�λ�ã����AOM����д�����̣�
���𰸡���1��25�㣻��2��40�㣻��3����AOM��180�㩁2����
��������
��1������![]() �Ķ������ɵõ�
�Ķ������ɵõ�![]() �Ķ�����
�Ķ�����
��2������OC�ǡ�MOB�Ľ�ƽ���ߣ����ɵõ�![]() �Ķ���������
�Ķ���������![]() ���ɵ�
���ɵ�![]() ��
��
��3��������ת��OCΪ![]() �Ľ�ƽ���ߣ����нǶȵļ��㼴�ɵõ�
�Ľ�ƽ���ߣ����нǶȵļ��㼴�ɵõ�![]() �Ķ���.
�Ķ���.
��1����![]() ��
��
��![]() ��
��
��2����OC��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��3����OC��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�
��![]() ��
��
��![]() ��
��

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д�����Ŀ���ڡ��ʶ��ߡ���Ŀ��Ӱ���£�ij��ѧ�����ڿ�չ�ˡ�������ҳɳ������黰������Ҫ�����Ҫϸ��������Ҫ����2���飬�����鳬��5������һ�꼶5���࣬��200��ѧ��������ʦΪ���˽�ѧ�������ڼҵĶ����������ȫ��ͬѧ������һ�������ҵ���˽��һ�꼶ѧ�����ڶ������.������λͬѧ���ԶԳ�һ�꼶������������˳������飬�������ݽ��������������Ƶ�ͳ��ͼ���ֱ�Ϊ��1����2����3.
��1���ڳ�һ�꼶���ѡ��5��ѧ�����ڶ��������ͳ�Ʊ�
�Ķ������������� | 2 | 3 | 4 | 5 |
���� | 2 | 1 | 1 | 1 |
��2���ڳ�һ�꼶���ж��ࡱ�����ѡȡ20��ѧ�����ڶ��������ͳ�Ʊ�
�Ķ������������� | 2 | 3 | 4 | 5 |
���� | 0 | 1 | 4 | 15 |
��3���ڳ�һ�꼶���ѡȡ20��ѧ�����ڶ��������ͳ�Ʊ�
�Ķ������������� | 2 | 3 | 4 | 5 |
���� | 2 | 8 | 6 | 4 |
����1���������ϲ��ϻش�����ͬѧ�У���һλͬѧ������ѡȡ������������Ҫ˵��������λͬѧѡȡ�����IJ���֮����
��ʦ�ֶԺ��������е�����ѧ�������ˡ��Ķ��������ĵ��У���������������ͳ��ͼ.
����2��ͨ��ͳ��ͼ����Ϣ����Ϊ���Ķ�������
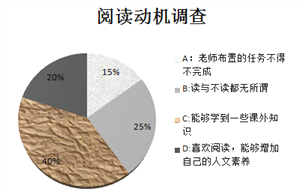
�ڡ�40%����Ⱥ�壬���ڶ�������Ŀ����Դ�˵���������.