题目内容
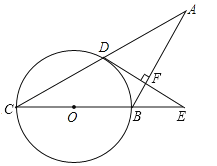
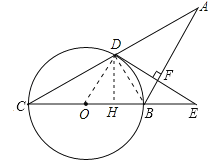
【题目】如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,tanC=![]() ,求EF的长.
,求EF的长.
【答案】(1)直线DE是⊙O的切线;(2)![]() .
.
【解析】试题分析:(1)连接圆心和切点,利用平行,OF⊥CB可证得∠ODF=90°;
(2)过D作DH⊥BC于H,设BD=k,CD=2k,求得BD、CD的长,根据三角形的面积公式得到DH的长,由勾股定理得到OH的长,根据射影定理得到OD2=OHOE,求得OE的长,从而得到BE的长,根据相似三角形的性质得到BF=2,根据勾股定理即可得到结论.
试题解析:解:(1)证明:如图,连接OD,BD,∵AB是⊙O的直径,∴∠ADB=∠90°,∴BD⊥AC.
∵AB=BC,∴AD=DC.∵OA=OB,∴OD∥BC,∵DE⊥BC,∴DE⊥OD,∴直线DE是⊙O的切线.
(2)过D作DH⊥BC于H,∵⊙O的半径R=5,tanC=![]() ,∴BC=10,设BD=k,CD=2k,∴BC=
,∴BC=10,设BD=k,CD=2k,∴BC=![]() k=10,∴k=2
k=10,∴k=2![]() ,∴BD=2
,∴BD=2![]() ,CD=4
,CD=4![]() ,∴DH=
,∴DH=![]() =4,∴OH=
=4,∴OH=![]() =3,∵DE⊥OD,DH⊥OE,∴OD2=OHOE,∴OE=
=3,∵DE⊥OD,DH⊥OE,∴OD2=OHOE,∴OE=![]() ,∴BE=
,∴BE=![]() ,∵DE⊥AB,∴BF∥OD,∴△BFE∽△ODE,∴
,∵DE⊥AB,∴BF∥OD,∴△BFE∽△ODE,∴![]() ,即
,即 ,∴BF=2,∴EF=
,∴BF=2,∴EF=![]() =
=![]() .
.

【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差( | |
初中部 | a | 85 | b |
|
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差![]() ,并判断哪一个代表队选手成绩较为稳定.
,并判断哪一个代表队选手成绩较为稳定.