��Ŀ����
����Ŀ����Сѧ������֪�������ξ��������������߶�������ĸ��ڽǶ���ֱ���������ʵ���������֪ʶ���������������
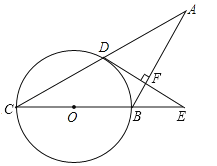
��֪����ͼ����������ABCD����AB=4����G������AB�ϵ�һ����������DGΪ��������������DGEF����EH��AB�ڵ�H��
��1���������AGD+��EGH=�� ������
��2������G�ڵ�B���ұ���
����֤����DAG�ա�GHE��
����̽����EH��BG��ֵ�Ƿ�Ϊ��ֵ���������������ֵ������������˵��������
��3������EB����G��������˶�����G���A�غϳ�����������������EBH�Ķ�����

���𰸡���1��90����2���ٴ𰸼���������EH��BG��ֵ�Ƕ�ֵ4����3��45����
�������������������1�����������ε����ʵõ���DGE=90�㣬��ƽ�ǵĶ��弴�ɵõ����ۣ�
��2���ٸ��ݴ�ֱ�Ķ���õ���GHE=90�㣬������ǵ����ʵõ���GEH=��AGD�����������ε����ʵõ���DAG=90�㣬DG=GE����á�DAG=��GHE������ȫ�������ε��ж��������ɵõ����ۣ��ڸ���ȫ�������ε����ʵõ�AG=EH�������߶εĺͲ�ɵõ����ۣ�
��3�����������������ۣ��� I������G�ڵ�B�����ʱ����ͼ1������ȫ�������ε����ʵõ�GH=DA=AB��EH=AG�����ǵõ�GB+BH=AG+GB���Ƴ���BHE�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʵõ���EBH=45�㣻�� II����ͼ2������G�ڵ�B���Ҳ�ʱ������ȫ�������ε���֪����GH=DA=AB��EH=AG�����ǵõ�AB+BG=BG+GH���Ƴ���BHE�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʵõ���EBH=45�㣻�� III������G���B�غ�ʱ����ͼ3������ȫ�������ε����ʵõ�GH=DA=AB��EH=AG=AB���Ƴ���GHE������BHE���ǵ���ֱ�������Σ����ǵõ���EBH=45�㼴�ɵõ����ۣ�
����������⣺ ��1��90��
��2���١�EH��AB��
���GHE![]() 90����
90����
���GEH+��EGH![]() 90����
90����
����AGD+��EGH![]() 90����
90����
���GEH![]() ��AGD��
��AGD��
���ı���ABCD���ı���DGEF���������Σ�
���DAG![]() 90����DG
90����DG![]() GE��
GE��
���DAG![]() ��GHE��
��GHE��
����DAG����GHE��
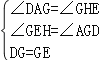 ��
��
���DAG�ա�GHE��AAS����
��EH��BG��ֵ�Ƕ�ֵ��
�������£�����֤�ã���DAG�ա�GHE��
��AG![]() EH��
EH��
��AG![]() AB
AB![]() BG��AB
BG��AB![]() 4��
4��
��EH![]() AB+BG��EH��BG
AB+BG��EH��BG![]() AB
AB![]() 4��
4��
��3�����������������ۣ�
��I������G�ڵ�B�����ʱ����ͼ1��
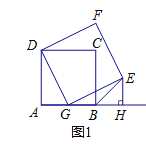
ͬ��2������֤�ã���DAG�ա�GHE��
��GH![]() DA
DA![]() AB��EH
AB��EH![]() AG��
AG��
��GB+BH![]() AG+GB��
AG+GB��
��BH![]() AG
AG![]() EH������GHE
EH������GHE![]() 90��
90��
���BHE�ǵ���ֱ�������Σ�
���EBH![]() 45����
45����
�� II�� ��ͼ2������G�ڵ�B���Ҳ�ʱ��
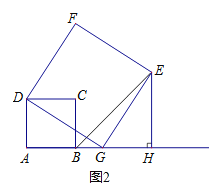
�ɣ�2����֤�ã���DAG�ա�GHE��
��GH![]() DA
DA![]() AB��EH
AB��EH![]() AG��
AG��
��AB+BG![]() BG+GH��
BG+GH��
��AG![]() BH����EH
BH����EH![]() AG
AG
��EH![]() HB������GHE
HB������GHE![]() 90��
90��
���BHE�ǵ���ֱ�������Σ�
���EBH![]() 45����
45����
�� III������G���B�غ�ʱ��
��ͼ3��ͬ����֤����DAG�ա�GHE��
��GH![]() DA
DA![]() AB��EH
AB��EH![]() AG
AG![]() AB��
AB��
���GHE������BHE���ǵ���ֱ�������Σ�
���EBH![]() 45��
45��
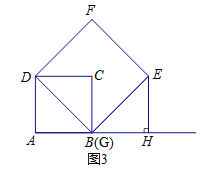
���ϣ���G��������˶�����G���A�غϳ��⣩�����У���EBH������45����