Question

【题目】已知，如图，∠ACB＝60°，∠ABC＝50°，BO、CO分别平分∠ABC、∠ACB，EF是经过点O且平行于BC的直线，求∠BOC的度数。

Answer 1

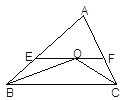
【答案】125°

【解析】试题分析：由∠ACB=60°，∠ABC=50°，BO，CO分别是∠ABC，∠ACB的平分线可以得到∠OBC、∠OCB的度数，又因为EF经过O点且平行BC，所以根据平行线性质可以求出∠EOB，∠FOC，而∠EOF是平角即180°，所以可以求出∠BOC．

试题解析：

∵BO，CO分别平分∠ABC，∠ACB，

∴∠OBC=∠ABC=×50°=25°，∠OCB=∠ACB=×60°=30°．

∵EF∥BC，

∴∠EOB=∠OBC=25°，∠FOC=∠OCB=30°．

又∵∠EOB+∠BOC+∠FOC=180°，

∴∠BOC=180°﹣∠EOB﹣∠FOC=180°﹣25°﹣30°=125 °．