题目内容
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作：
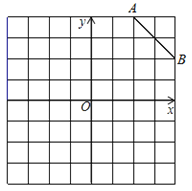
⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(2，4)，B点坐标为(4，2)；
⑵ 请在（1）中建立的平面直角坐标系的第一象限内的格点上确定点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是 ， △ABC的周长是 (结果保留根号)；
⑶ 以（2）中△ABC的点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.
【答案】（1）画图见解析；（2）画图见解析，C（1，1），△ABC的周长为（2
+2
）；（3）画图见解析，四边形ABA′B′是矩形，理由见解析．
【解析】（1）根据题意画出平面直角坐标系即可；（2）作线段AB的垂直平分线，与格点相交于点C，满足腰长为无理数，则C点即为所求点，求出AC、BC，即可得出△ABC的周长；（3）先画出图形，结合图形即可作出判断．
（1）如图所示：
（2）如图所示：
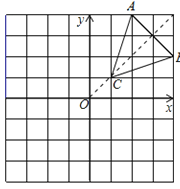
则AC=BC= 10 ，点C坐标为（1，1），△ABC的周长为（2
+2
）
（3）如图所示：
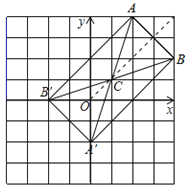
四边形ABA′B′是矩形．
“点睛”本题考查旋转作图的知识，解答本题的关键是掌握旋转变换的特点，难度一般．
练习册系列答案
相关题目
