题目内容
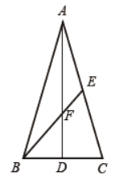
【题目】已知:如图,在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,点
,点![]() 、
、![]() 的横坐标是一元二次方程
的横坐标是一元二次方程![]() 的两根(
的两根(![]() ),直线
),直线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
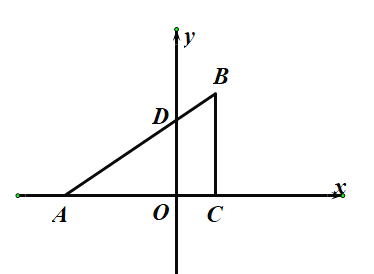
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)在![]() 轴上找一点
轴上找一点![]() ,连接
,连接![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似(不包括全等),并求点
相似(不包括全等),并求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,连接
上的动点,连接![]() ,点
,点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,以每秒1个单位长度的速度运动,当点
同时出发,以每秒1个单位长度的速度运动,当点![]() 到达点
到达点![]() 时,两点停止运动,设运动时间为
时,两点停止运动,设运动时间为![]() 秒,请直接写出几秒时以点
秒,请直接写出几秒时以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)解方程得到点A、C的坐标,根据点D的坐标设直线![]() 解析式为
解析式为![]() ,
,
将点A坐标代入即可得到直线AB的解析式;
(2)过![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,求出点B的坐标,根据
,求出点B的坐标,根据![]() 得到对应线段成比例,由此求出AE,即可得到点E的坐标;
得到对应线段成比例,由此求出AE,即可得到点E的坐标;
(3)由题意得到![]() ,
,![]() ,分两种情况:
,分两种情况:![]() ,
,![]() ,列比例式即可求出答案.
,列比例式即可求出答案.
解:(1)![]() ,
,
(x+3)(x-1)=0,
∴![]() ,
,![]() ,
,
∵点![]() 、
、![]() 的横坐标是一元二次方程
的横坐标是一元二次方程![]() 的两根,
的两根,
∴点![]() 、
、![]() 的横坐标分别为-3,1,即点
的横坐标分别为-3,1,即点![]() ,点
,点![]() ,
,
设直线![]() 解析式为
解析式为![]() ,且过点
,且过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 解析式:
解析式:![]() ;
;
(2)如图:过![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,
,
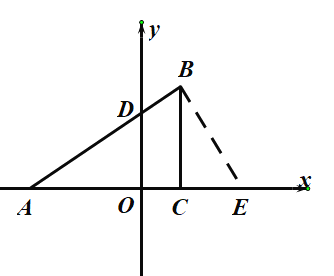
当![]() 时,则
时,则![]() ,∴点
,∴点![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ;
;
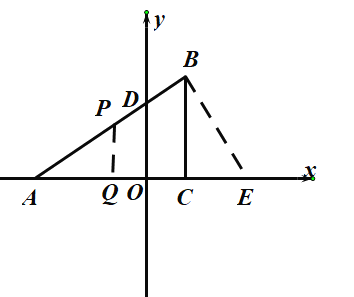
(3)由题意可得:![]() ,
,![]() 如图:
如图:
若![]() ,
,
∴![]() ,
,
∴ ,
,
∴![]() ;
;
如图:若![]() ,
,
∴![]() ,
,
∴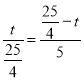 ,
,
∴![]() ,
,

综上所述:![]() 或
或![]() 时以点
时以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目