题目内容
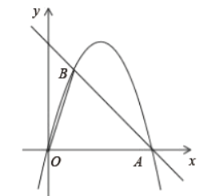
【题目】如图,在直角坐标平面内,抛物线经过原点![]() 、点
、点![]() ,又与
,又与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,过点
上的一点,过点![]() 作
作![]() ,与抛物线交于点
,与抛物线交于点![]() ,且点
,且点![]() 在第一象限内.
在第一象限内.
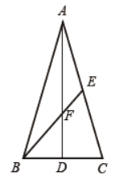
备用图
(1)求抛物线的表达式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)过点![]() 作
作![]() 轴,分别交直线
轴,分别交直线![]() 、
、![]() 轴于点
轴于点![]() 、
、![]() ,若
,若![]() 的面积等于
的面积等于![]() 的面积的
的面积的![]() 倍,求
倍,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
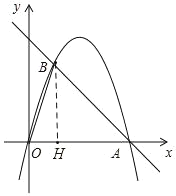
(1)过点B作BH⊥x轴,垂足为点H,根据等腰直角三角形的性质可求点A(4,0),用待定系数法可求抛物线的表达式;
(2)根据平行线的性质可得BM//OA,可求点M坐标,用待定系数法可求直线BO,直线AB,直线PM的解析式,即可求点P坐标;
(3)延长MP交x轴于点D,作PG⊥MN于点G,根据等腰直角三角形的性质可得AC=CN,PG=NG,根据锐角三角函数可得tan∠BOA=3=tan∠MPG=![]() ,可得MG=3PG=3NG,根据面积关系可求
,可得MG=3PG=3NG,根据面积关系可求![]() 的值.
的值.
解:(1)
过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() 抛物线过原点
抛物线过原点![]() 、点
、点![]() 、
、![]()
![]() 设抛物线的表达式为
设抛物线的表达式为![]()
![]()
![]()
![]()
![]() 抛物的线表达式为
抛物的线表达式为![]()
(2)
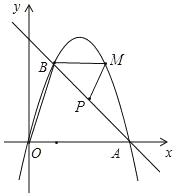
![]()
![]() 又
又![]()
`![]()
![]()
![]()
![]() 设
设![]()
![]() 在抛物线
在抛物线![]() 上
上![]()
![]() 直线
直线![]() 经过点
经过点![]() 、
、![]()
![]() 直线
直线![]() 的表达式为
的表达式为![]()
![]() 且直线
且直线![]() 过点
过点![]()
![]() 直线
直线![]() 的表达式为
的表达式为![]()
![]() 直线
直线![]() 经过点
经过点![]() 、
、![]()
![]() 直线
直线![]() 的表达式为
的表达式为![]()
![]()
![]()
(3)延长![]() 交
交![]() 轴于点
轴于点![]() ,作
,作![]() ,垂足为点
,垂足为点![]()
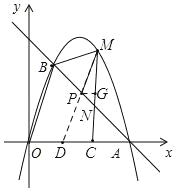
![]()
![]() ,
,![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
设![]() ,则
,则![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目