题目内容
已知,如图,正比例函数y=ax的图象与反比例函数y=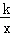 的图象交于点A(3,2)
的图象交于点A(3,2)

(1)填空:a= ;k= .
(2)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
①当BM=DM时,求△ODM的面积;
②当BM=2DM时,求出直线MA的解析式.
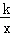 的图象交于点A(3,2)
的图象交于点A(3,2)
(1)填空:a= ;k= .
(2)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
①当BM=DM时,求△ODM的面积;
②当BM=2DM时,求出直线MA的解析式.
(1) 6(2)①3 ②y=﹣x+5
6(2)①3 ②y=﹣x+5
 6(2)①3 ②y=﹣x+5
6(2)①3 ②y=﹣x+5试题分析:(1)将A的坐标代入正比例函数解析式中,求出a的值;将A坐标代入反比例解析式中,即可求出k的值;
(2)①由A的横坐标为3,得到BD=3,当BM=DM时,求出m的值,将m代入反比例解析式中求出n的值,确定出M坐标,三角形ODM以MD为底边,OB为高,利用三角形的面积公式求出即可;
②由BM=2DM及BD=3,求出m的长,将m的值代入反比例解析式中求出n的值,确定出M坐标,设直线AM的解析式为y=kx+b,将A与M的坐标代入得到关于k与b的方程组,求出方程组的解得到k与b的值,即可求出直线AM的解析式.
解:(1)将A的坐标代入正比例函数y=ax中得:2=3a,解得:a=
 ;
;将A坐标代入反比例函数y=
 中得:2=
中得:2= ,解得:k=6;
,解得:k=6;故答案为:
 ;6;
;6;(2)①由已知得BD=3,当BM=DM时,m=
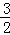 ,
,当x=
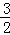 时,y=4,则S△ODM=
时,y=4,则S△ODM= ×
×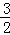 ×4=3;
×4=3; ②由已知得BD=3,当BM=2DM时,m=3×
 =2,
=2,当x=2时,y=3,即M(2,3),
设直线MA的解析式为y=kx+b,
将A(3,2),M(2,3)代入得:
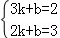 ,
,解得:
 ,
,∴y=﹣x+5.
点评:此题考查了反比例函数与一次函数的交点问题,涉及的知识有:待定系数法确定函数解析式,以及坐标与图形性质,灵活运用待定系数法是解本题的关键.

练习册系列答案
相关题目
 的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点.已知当x>1时,y1>y2;当0<x<1时,y1<y2.
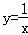 (x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .
(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE,则b= .
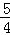 m3
m3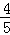 m3
m3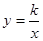 (k<0)的图象上有三点A1(x1, y1 )、A2(x2, y2)、A3(x3, y3 ),已知x1<x2<0<x3,则下列各式中,正确的是 ( )
(k<0)的图象上有三点A1(x1, y1 )、A2(x2, y2)、A3(x3, y3 ),已知x1<x2<0<x3,则下列各式中,正确的是 ( )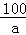
 交于点A、B,则不等式组
交于点A、B,则不等式组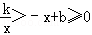 的解集为( )
的解集为( )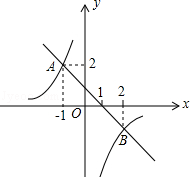
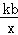 在同一坐标系中的大致图象正确的是( )
在同一坐标系中的大致图象正确的是( )