题目内容
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,
)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
(1)求直线AB的解析式;
(2)若S△ACD=
,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三角形与△OBA相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.

| 3 |
(1)求直线AB的解析式;
(2)若S△ACD=
| ||
| 6 |
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三角形与△OBA相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.

(1)设直线AB的解析式为y=kx+b,
∵A(3,0),B(0,
),
∴
,解得
,
∴直线AB的解析式为y=-
x+
;
(2)设点C的坐标为(x,-
x+
),则0≤x≤3,OD=x,AD=OA-OD=3-x,CD=-
x+
,
∵S△ACD=
,
∴
(3-x)(-
x+
)=
,
整理,得x2-6x+8=0,
解得x1=2,x2=4(不合题意舍去),
∴C的坐标为(2,
);
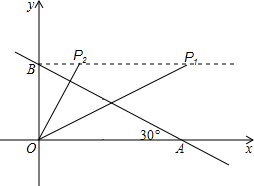 (3)以P,O,B为顶点的三角形与△OBA相似时,分三种情况:
(3)以P,O,B为顶点的三角形与△OBA相似时,分三种情况:
①当∠OBP=90°时,如图.
若△BPO∽△OAB,则∠BPO=∠OAB=30°,BP=
OB=3,
∴P1(3,
);
若△BOP∽△OAB,则∠BOP=∠OAB=30°,BP=
OB=1,
∴P2(1,
);
②当∠OPB=90°时,如图.
过点O作OP⊥BA于点P,过点P作PM⊥OA于点M.
若△PBO∽△OBA,则∠BOP=∠BAO=30°,
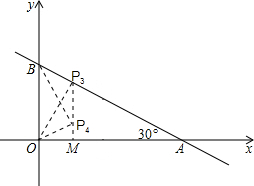 在Rt△PBO中,BP=
在Rt△PBO中,BP=
OB=
,OP=
BP=
.
∵在Rt△PMO中,∠OPM=30°,
∴OM=
OP=
,PM=
OM=
,
∴P3(
,
);
若△POB∽△OBA,则∠OBP=∠BAO=30°,∠POM=30°.
∴PM=
OM=
,
∴P4(
,
);
③当∠POB=90°时,点P在x轴上,不符合要求.
综合所述,符合条件的点有四个,分别是:P1(3,
),P2(1,
),P3(
,
),P4(
,
).
∵A(3,0),B(0,
| 3 |
∴
|
|
∴直线AB的解析式为y=-
| ||
| 3 |
| 3 |
(2)设点C的坐标为(x,-
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
∵S△ACD=
| ||
| 6 |
∴
| 1 |
| 2 |
| ||
| 3 |
| 3 |
| ||
| 6 |
整理,得x2-6x+8=0,
解得x1=2,x2=4(不合题意舍去),
∴C的坐标为(2,
| ||
| 3 |
 (3)以P,O,B为顶点的三角形与△OBA相似时,分三种情况:
(3)以P,O,B为顶点的三角形与△OBA相似时,分三种情况:①当∠OBP=90°时,如图.
若△BPO∽△OAB,则∠BPO=∠OAB=30°,BP=
| 3 |
∴P1(3,
| 3 |
若△BOP∽△OAB,则∠BOP=∠OAB=30°,BP=
| ||
| 3 |
∴P2(1,
| 3 |
②当∠OPB=90°时,如图.
过点O作OP⊥BA于点P,过点P作PM⊥OA于点M.
若△PBO∽△OBA,则∠BOP=∠BAO=30°,
 在Rt△PBO中,BP=
在Rt△PBO中,BP=| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
∵在Rt△PMO中,∠OPM=30°,
∴OM=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
3
| ||
| 4 |
∴P3(
| 3 |
| 4 |
3
| ||
| 4 |
若△POB∽△OBA,则∠OBP=∠BAO=30°,∠POM=30°.
∴PM=
| ||
| 3 |
| ||
| 4 |
∴P4(
| 3 |
| 4 |
| ||
| 4 |
③当∠POB=90°时,点P在x轴上,不符合要求.
综合所述,符合条件的点有四个,分别是:P1(3,
| 3 |
| 3 |
| 3 |
| 4 |
3
| ||
| 4 |
| 3 |
| 4 |
| ||
| 4 |

练习册系列答案
相关题目


 )与时间x(小时)的函数图象,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙工作.
)与时间x(小时)的函数图象,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙工作. 线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒
线段AO上以每秒1个单位长度的速度向点O移动,设点Q,P移动的时间为t秒

 p(千帕)随温度t(℃)变化的函数关系式是P=kt+b,其图象是如图所示的射线AB.
p(千帕)随温度t(℃)变化的函数关系式是P=kt+b,其图象是如图所示的射线AB.