Question

线段AB，其中点A（1，-4），点B（5，-4），将线段AB绕中点C逆时针旋转30°后，得到新的线段A′B′，则线段A′B′的解析式为______．

Answer 1

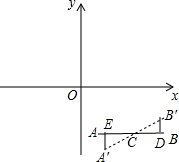
如图，过A′、B′分别作AB的垂线，垂足分别为E、D，
∵点A（1，-4），点B（5，-4），C为AB的中点，
∴AB=4，C点坐标为（3，-4），
∵线段AB绕中点C逆时针旋转30°后，得到新的线段A′B′，
∴∠A′CE=∠B′CD=30°，CA′=CB′=CB=2，
∴B′D=1，CD=CE=

3

，
∴B′的坐标为（3+

3

，-3）
设线段A′B′的解析式为y=kx+b，
把C（3，-4）、B′（3+

3

，-3）代入

3k+b=-4 (3+ 3 )k+b=-3

，解得

k= 3 3 b=-4- 3

，
∴线段A′B′的解析式为y=

3

3

x-4-

3

（3-

3

≤x≤3+

3

）．
故答案为y=

3

3

x-4-

3

（3-

3

≤x≤3+

3

）．