题目内容
如图,四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形.点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是(
,
),则k+b=______.

| 19 |
| 4 |
| 9 |
| 4 |

由于A3B3C3C2为正方形,点B3的坐标是(
,
),所以正方形A3B3C3C2的边长为
,于是A3坐标为(
-
,
)即(
,
).
设OC1=C1B1=x,C1C2=C2B2=
-x,易得△A1B1A2∽△A2B2A3,所以
=
,
即
=
,
解得x1=1,x2=
>
(舍去).A2坐标为(1,
-1),即(1,
),
代入y=kx+b得k+b=
.
| 19 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 19 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 10 |
| 4 |
| 9 |
| 4 |
设OC1=C1B1=x,C1C2=C2B2=
| 10 |
| 4 |
| A3B2 |
| A2B2 |
| A2B1 |
| A1B1 |
即
| ||||
|
| ||
| x |
解得x1=1,x2=
| 25 |
| 4 |
| 9 |
| 4 |
| 10 |
| 4 |
| 3 |
| 2 |
代入y=kx+b得k+b=
| 3 |
| 2 |

练习册系列答案
相关题目


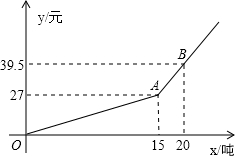 )与用水量x(吨)的函数关系如图所示.
)与用水量x(吨)的函数关系如图所示. C,点D是直线AC上的一个动点.
C,点D是直线AC上的一个动点.





 在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.