题目内容
【题目】几何探究:
(问题发现)
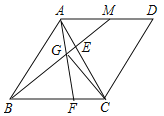
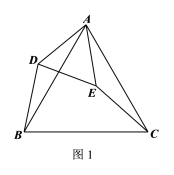
(1)如图1所示,△ABC和△ADE是有公共顶点的等边三角形,BD、CE的关系是_______(选填“相等”或“不相等”);(请直接写出答案)
(类比探究)
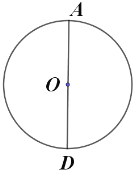
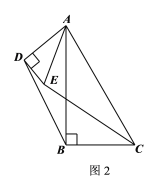
(2)如图2所示,△ABC和△ADE是有公共顶点的含有![]() 角的直角三角形,(1)中的结论还成立吗?请说明理由;
角的直角三角形,(1)中的结论还成立吗?请说明理由;
(拓展延伸)
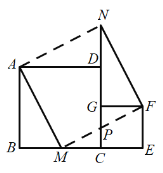
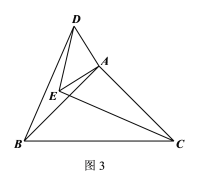
(3)如图3所示,△ADE和△ABC是有公共顶点且相似比为1 : 2的两个等腰直角三角形,将△ADE绕点A自由旋转,若![]() ,当B、D、E三点共线时,直接写出BD的长.
,当B、D、E三点共线时,直接写出BD的长.
【答案】(1)相等;(2)不成立,理由见解析;(3)![]() 或
或![]() .
.
【解析】
(1)证明△ABD≌△ACE(SAS),即可得出![]() ;
;
(2)当在Rt△ADE和Rt△ABC中,![]() ,证明△ABD∽△ACE,求出BD与CE的比例;
,证明△ABD∽△ACE,求出BD与CE的比例;
(3)分两种情况求出BD的长即可.
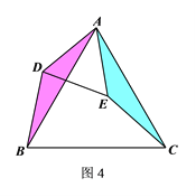
(1)相等;
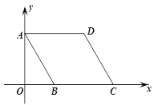
提示:如图4所示.
∵△ADE和△ABC均为等边三角形,
∴![]()
![]()
∴![]()
∴![]()
在△ABD和△ACE中,
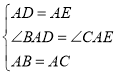
∴△ABD≌△ACE(SAS)
∴![]() .
.
(2)不成立;
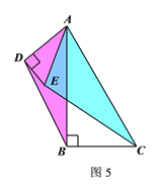
理由如下:如图5所示.
在Rt△ADE和Rt△ABC中,
∵![]()
∴![]()
![]()
∴![]()
∵![]()
∴△ABD∽△ACE
∴![]()
∴![]()
故(1)中的结论不成立;
(3)![]() 或
或![]() .
.
提示:分为两种情况:
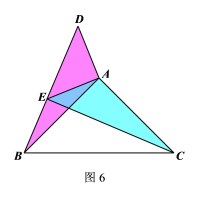
①如图6所示.
易证:△ABD≌△ACE(SAS)
∴![]()
∴![]()
∴![]()
由题意可知:![]()
设![]() ,则
,则![]()
在Rt△BCE中,由勾股定理得:
![]()
∴![]()
解之得:![]() (
(![]() 舍去)
舍去)
∴![]() ;
;
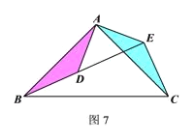
②如图7所示.
易证:△ABD≌△ACE(SAS),![]()
设![]() ,则
,则![]()
在Rt△BCE中,由勾股定理得:
![]()
∴![]()
解之得:![]() (
(![]() 舍去)
舍去)
∴![]() .
.
综上所述,![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目