题目内容
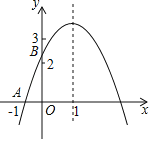
【题目】关于二次函数y=mx2+(2m+4)x+8(m为常数,且m≠0),
(1)证明:该函数与x轴一定有交点;
(2)若该函数经过点A(﹣1+![]() ,y1)B(﹣1,y2),请比较y1,y2的大小关系,并说明理由.
,y1)B(﹣1,y2),请比较y1,y2的大小关系,并说明理由.
【答案】(1)见解析;(2)当m>0时, y1>y2;当m<0时, y2>y1.
【解析】
(1)证得△=(2m+4)232m=(2m4)2≥0,则函数与x轴一定有交点;
(2)函数的对称轴为x=﹣1﹣![]() ,当m>0时,﹣1+
,当m>0时,﹣1+![]() >﹣1>﹣1﹣
>﹣1>﹣1﹣![]() ,y随x的增大而增大,所以y1>y2;当m<0时,﹣1﹣
,y随x的增大而增大,所以y1>y2;当m<0时,﹣1﹣![]() >﹣1>﹣1+
>﹣1>﹣1+![]() ,y随x的增大而增大,所以y2>y1;
,y随x的增大而增大,所以y2>y1;
(1)二次函数y=mx2+(2m+4)x+8,
△=(2m+4)2﹣32m=4m2﹣32m+16=(2m﹣4)2≥0,
∴函数与x轴一定有交点;
(2)函数的对称轴为x=﹣1﹣![]() ,
,
当m>0时,﹣1+![]() >﹣1>﹣1﹣
>﹣1>﹣1﹣![]() ,
,
∴y随x的增大而增大,
∴y1>y2;
当m<0时,﹣1﹣![]() >﹣1>﹣1+
>﹣1>﹣1+![]() ,
,
y随x的增大而增大,
∴y2>y1.

练习册系列答案
相关题目
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )
姓名 | 小红 | 小明 | 小东 | 小亮 | 小丽 | 小华 |
成绩(分) | 110 | 106 | 109 | 111 | 108 | 110 |
A.众数是110B.方差是16
C.平均数是109.5D.中位数是109