题目内容
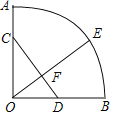
【题目】如图，点D是等边△ABC内一点，将△DBC绕点B旋转到△EBA的位置，则∠EBD的度数是（ ）
A. 45°B. 60°C. 90°D. 120°
【答案】B
【解析】
由将△DBC绕点B旋转到△EBA的位置，即可得△DBC≌△EBA，根据全等三角形的性质可得∠ABE=∠CBD，又由△ABC是等边三角形，可得∠ABC=60°，继而由∠EBD=∠ABE+∠ABD=∠CBD+∠ABD=∠ABC，求得∠EBD的度数．
解：∵将△DBC绕点B旋转到△EBA的位置，
∴△DBC≌△EBA，
∴∠ABE=∠CBD，
∵△ABC是等边三角形，
∴∠ABC=60°，
∴∠EBD=∠ABE+∠ABD=∠CBD+∠ABD=∠ABC=60°．
故选B．
练习册系列答案
口算题天天练系列答案
相关题目
【题目】今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．
评估成绩n（分） | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n＜90 | B | |
70≤n＜80 | C | 15 |
n＜70 | D | 6 |
根据以上信息解答下列问题：
（1）求m的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）
（3）从评估成绩不少于80分的连锁店中任选2家介绍营销经验，求其中至少有一家是A等级的概率．
