题目内容
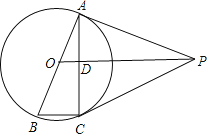
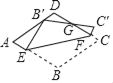
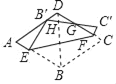
【题目】如图,在菱形紙片ABCD中,AB=2.将纸片折叠,使点B落在AD边上的点B′处(不与A,D重合),点C落在C′处,线段B′C′与直线CD交于点G,折痕为EF,则下列说法:①若∠A=90,B′为AD中点时,AE=![]() ;②若∠A=60°,B′为AD中点时,点E恰好是AB的中点;③若∠A=60°,C′F⊥CD时,
;②若∠A=60°,B′为AD中点时,点E恰好是AB的中点;③若∠A=60°,C′F⊥CD时,![]() ,其中正确的是( )
,其中正确的是( )
A.①②B.①③C.②③D.①②③
【答案】D
【解析】
①证出四边形ABCD是正方形,得出AB=AD,设AE=x,则B'E=BE=2x,在Rt△AB'E中,由勾股定理得出方程,解方程即可;
②连接BD、BE',证出△ABD是等边三角形,由等边三角形的性质得出∠AB'B=90°,∠ABB'=30°,证出△AB'E是等边三角形,得出AE=B'E=BE即可;
③设CF=x,由折叠的性质得:C'F=CF=x,∠C'=∠C=∠A=60°,得出∠C'GF=30°,得出C'G=2C'F=2x,GF=![]() C'F=
C'F=![]() x,则DG=CDGFCF=2
x,则DG=CDGFCF=2![]() xx,证出DB'=DG,作DH⊥B'C'于H,则B'H=GH=12B'G=12(22x)=1x,得出DG=
xx,证出DB'=DG,作DH⊥B'C'于H,则B'H=GH=12B'G=12(22x)=1x,得出DG=![]() ,得出方程
,得出方程![]() =2﹣
=2﹣![]() x﹣x,解得x=4﹣2
x﹣x,解得x=4﹣2![]() ,得出CF=4﹣2
,得出CF=4﹣2![]() ,FD=2﹣(4﹣2
,FD=2﹣(4﹣2![]() )=2
)=2![]() ﹣2,即可得出结果.
﹣2,即可得出结果.
①∵∠A=90°,四边形ABCD是菱形,
∴四边形ABCD是正方形,
∴AB=AD,
∵B′为AD中点时,
∴AB'=1,
设AE=x,则B'E=BE=2﹣x,
在Rt△AB'E中,由勾股定理得:12+x2=(2﹣x)2,
解得:x=![]() ,①正确;
,①正确;
②连接BD、BE',如图:
∵∠A=60°,AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵B′为AD中点,
∴∠AB'B=90°,∠ABB'=30°∵BE=B'E,
∴∠BB'E=∠ABB'=30°,
∴∠AB'E=60°,
∴△AB'E是等边三角形,
∴AE=B'E=BE,
∴点E是AB的中点,②正确;
③设CF=x,
由折叠的性质得:C'F=CF=x,∠C'=∠C=∠A=60°,
∵C′F⊥CD,
∴∠C'GF=30°,
∴C'G=2C'F=2x,GF=![]() C'F=
C'F=![]() x,
x,
∴DG=CD﹣GF﹣CF=2﹣![]() x﹣x,
x﹣x,
∵∠D=180°﹣∠A=120°,∠DGB'=∠C'GF=30°,
∴∠DB'G=30°,
∴DB'=DG,
设BD交B'C'于H,则B'H=GH=![]() B'G=
B'G=![]() (2﹣2x)=1﹣x,
(2﹣2x)=1﹣x,
∴DG=![]() ,∴
,∴![]() =2﹣
=2﹣![]() x﹣x,
x﹣x,
解得:x=4﹣2![]() ,
,
∴CF=4﹣2![]() ,FD=2﹣(4﹣2
,FD=2﹣(4﹣2![]() )=2
)=2![]() ﹣2,
﹣2,
∴![]() ,③正确;
,③正确;
故选:D.

【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
表1:四种款式电脑的利润
电脑款式 | A | B | C | D |
利润(元/台) | 160 | 200 | 240 | 320 |
表2:甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量(台) | 20 | 15 | 10 | 5 |
乙店销售数量(台)8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识,解决下列问题:
(1)从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为 ;
(2)经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.
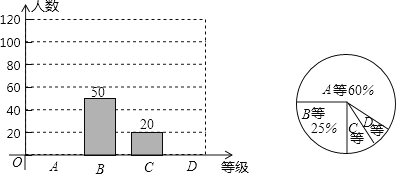
【题目】某校九年级教师在某班随机抽查了学生报考志愿的情况,绘制了如下扇形图和统计表,学生统计表绘制好后不小心撕掉了一个角.
报考学校 | 一中 | 二中 | 八中 | 其他 |
报考人数 | 4 | 5 | 6 |
(1)求撕掉角上的数和抽查学生的总数;
(2)老师打算从抽查的学生中随机抽取1个人来谈感想,求抽到报考一中学生的概率;
(3)把抽查学生的人数看做一组数据,抽查学生报考志愿人数的众数是 ,报考志愿的人数中位数是 .
(4)报考一中的人数百分比在扇形统计图中所占圆心角的正切值为 ,报考八中的百分比所占扇形统计图的圆心角的度数是 .(注:tan36°≈0.7265;tan72°≈3.078;)