题目内容
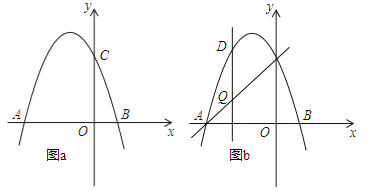
【题目】如图，抛物线
交x轴于点A（﹣3，0）和点B，交y轴于点C（0，3）．
（1）求抛物线的函数表达式；
（2）若点P在抛物线上，且
，求点P的坐标；
（3）如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值．
【答案】（1）
；（2）P（﹣1，4），
，
；（3）
．
【解析】
（1）把点A、C的坐标分别代入函数解析式，解方程组即可得到结论；
（2）设P点坐标为（x，
），根据
列出关于x的方程，解方程求出x的值，进而得到点P的坐标；
（3）先求出直线AC的解析式为y=x+3，再设Q点坐标为（x，x+3），则D点坐标为（x，），然后用含x的代数式表示QD，根据二次函数的性质即可求出线段QD长度的最大值．
（1）把A（﹣3，0），C（0，3）代入
，得：
，解得：
，故该抛物线的解析式为：；
（2）由（1）知，该抛物线的解析式为，则易得B（1，0），设P点坐标为（x，），∵，∴
，整理，得
或
，解得x=﹣1或x=
，则符合条件的点P的坐标为：（﹣1，4），
，
；
（3）设直线AC的解析式为
，将A（﹣3，0），C（0，3）代入，得：
，解得：
，即直线AC的解析式为
．设Q点坐标为（x，x+3），（﹣3≤x≤0），则D点坐标为（x，），QD=
=
=
，∴当x=
时，QD有最大值．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
