题目内容
【题目】如图，边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动（A、D都不与坐标原点O重合），作CE⊥x轴，垂足为E，当OA等于 时，四边形OACE面积最大．
【答案】
．
【解析】
试题解析：∵四边形ABCD是正方形，
∴DA=DC，∠ADC=90°．
∵∠AOD=90°，CE⊥y轴，
∴∠AOD=∠DEC=90°，∠ADO=∠DCE=90°-∠CDE．
在△AOD和△DEC中，
，
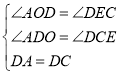∴△AOD≌△DEC，
∴AO=DE，OD=EC．
设OA=x，OD=y，
则有DE=OA=x，CE=OD=y，x2+y2=16，
∴S四边形OECA=
（x+y）2=（x2+y2+2xy）
=（16+2xy）
=8+xy
=8+ [x2+y2-（x-y）2]
=8+[16-（x-y）2]
=16-（x-y）2
当x=y时，S四边形OECA取到最大值，
此时OA=OD=4×
=．
练习册系列答案
相关题目
