题目内容
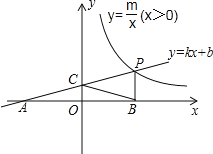
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(1,t+1),B(t-5,-1)两点.
的图象交于A(1,t+1),B(t-5,-1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若点(c,p)和(n,q)是反比例函数y=![]() 图象上任意两点,且满足c=n+1时,求
图象上任意两点,且满足c=n+1时,求![]() 的值.
的值.
(3)若点M(x1,y1)和N(x2,y2)在直线AB(不与A、B重合)上,过M、N两点分别作y轴的平行线交双曲线于E、F,已知x1<-3,0<x2<1,当x1x2=-3时,判断四边形NFEM的形状.并说明理由.

【答案】(1)反比例函数的解析式为y=![]() ,一次函数解析式为y=x+2;(2)
,一次函数解析式为y=x+2;(2)![]() ;(3)四边形MNFE为平行四边形,理由见解析
;(3)四边形MNFE为平行四边形,理由见解析
【解析】
(1)根据反比例函数的定义,求出t的值,然后得到点A和点B的坐标,利用待定系数法进行求解,即可得到答案;
(2)根据反比例函数的定义,表示出c和n的值,由c=n+1,代入计算,即可得到答案;
(3)先由点的坐标,得到ME和NF的长度,利用作差法证明两条线段相等,然后根据一组对边平行且相等即可证明是平行四边形.
解:(1)∵A(1,t+1),B(t﹣5,﹣1)两点在反比例函数y=![]() 的图象上,
的图象上,
∴t+1=﹣(t﹣5)=m,
即t+1=5﹣t,
解得t=2.
当t=2时,A(1,3),B(﹣3,﹣1),
∴m=3,
∴反比例函数的解析式为:y=![]() .
.
∵A、B在一次函数y=kx+b的图象上,
∴![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为:y=x+2;
(2)∵点(c,p)和(n,q)在反比例函数y=![]() 图象上,
图象上,
∴cp=nq=m=3
c=![]() ,n=
,n=![]()
∵c=n+1,
∴![]() ,
,
∴![]() ;
;
(3)四边形MNFE为平行四边形,
由题意可知,M(x1,x1+2),N(x2,x2+2),E(x1,![]() ),F(x2,
),F(x2,![]() ),
),
即ME=x1+2﹣![]() ,NF=x2+2﹣
,NF=x2+2﹣![]() ,
,
∵ME﹣NF=(x1+2﹣![]() )-(x2+2﹣
)-(x2+2﹣![]() )
)
即ME﹣NF=(x1﹣x2)(1+![]() )
)
∵x1<﹣3,0<x2<1,
∴x1﹣x2≠0,
∵x1x2=﹣3
∴1+![]() =0,
=0,
∴ME﹣NF=0,
即ME=NF
又∵ME∥NF,
∴四边形MNFE为平行四边形