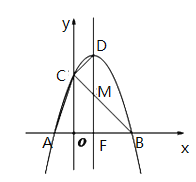Question

【题目】如图，已知二次函数 的图象M经过(，0)，(2，)两点且与轴的另一个交点为．

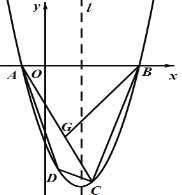
（1）求该二次函数的解析式；

（2）点是线段上的动点（点G与线段的端点不重合），若△AGB∽△ABC，求点G的坐标；

（3）设抛物线的对称轴为，点是抛物线上一动点，当△ACD的面积为时，点D关于的对称点为E，能否在抛物线和上分别找到点P、Q，使得以点D、E、P、Q为顶点的四边形为平行四边形. 若能，求出点P的坐标；若不能，请说明理由．

Answer 1

【答案】（1）；（2）点G的坐标为；（3）能. 点P的坐标为或．

【解析】

（1）把点A、C坐标代入二次函数的表达式，即可求解；

（2）先求出直线AC的解析式，设点G的坐标为，根据勾股定理求出AC、AG，再由三角形相似对应边成比例求出k的值，进而得到答案；

（3）过D点作的垂线交于点H，根据=，列方程求出m的值，进而求出点D的坐标，再根据以点D、E、P、Q为顶点的四边形为平行四边形，则∥且，求得点 Q的坐标，进而求得点P的纵坐标．

（1）∵二次函数的图象经过A(，0)，C(2，)两点，

∴解得 .

∴二次函数的解析式为

（2）∵A(，0)，C(2，)∴线段AC的解析式：.

设点G的坐标为.

由可知：B(4,0)

∴AB=5，

AG=

∵△AGB∽△ABC，

∴

∴

∴

∴或（舍去）

∴点G的坐标为

（3）能. 理由如下：如答图，过D点作的垂线交于点H，

∵， ∴.

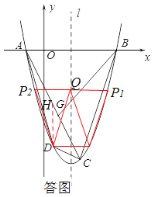
∵点是抛物线上一动点，上，

∴.

∵△ACD的面积为，

∴，

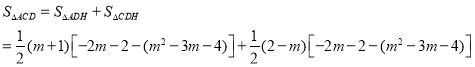
整理得，解得.

∴.

∵，∴图象的对称轴为.

∵点D关于的对称点为E，∴

∴.

若以点D、E、P、Q为顶点的四边形为平行四边形，则∥且.

∵Q在对称轴x=上，

∴Q的横坐标为，

∴点P的横坐标为或.

∴当x=或时，点P的纵坐标为.

∴点P的坐标为或.