题目内容
 已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是
已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是
- A.①③
- B.②④
- C.①③④
- D.①②③④
D
分析:在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答:①∵∠1=∠2,
∴a∥b(同位角相等,两直线平行).
②∵∠3=∠6,
∴a∥b(内错角相等,两直线平行).
③∵∠4+∠7=180°,
∵∠4=∠6(对顶角相等),
∴∠6+∠7=180°,
∴a∥b(同旁内角互补,两直线平行).
④同理得,a∥b(同旁内角互补,两直线平行).
故选D.
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
分析:在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答:①∵∠1=∠2,
∴a∥b(同位角相等,两直线平行).
②∵∠3=∠6,
∴a∥b(内错角相等,两直线平行).
③∵∠4+∠7=180°,
∵∠4=∠6(对顶角相等),
∴∠6+∠7=180°,
∴a∥b(同旁内角互补,两直线平行).
④同理得,a∥b(同旁内角互补,两直线平行).
故选D.
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
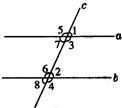 7、已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )
7、已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )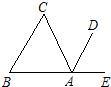 23、已知:如图所示,直线AD∥BC,AD平分∠CAE,求证:∠B=∠C.
23、已知:如图所示,直线AD∥BC,AD平分∠CAE,求证:∠B=∠C.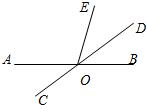 4、已知:如图所示,直线AB、CD相交于O,OD平分∠BOE,∠AOC=42°,则∠AOE的度数为( )
4、已知:如图所示,直线AB、CD相交于O,OD平分∠BOE,∠AOC=42°,则∠AOE的度数为( )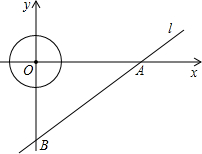 已知:如图所示,直线l的解析式为
已知:如图所示,直线l的解析式为 已知:如图所示,直线AB∥CD,CO⊥OD于O点,并且∠1=40度.则∠D的度数是( )
已知:如图所示,直线AB∥CD,CO⊥OD于O点,并且∠1=40度.则∠D的度数是( )