题目内容
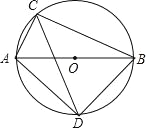
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
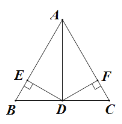
(1)求证:AB=AC;
(2)若∠BAC=60°,BC=6,求△ABC的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)由角平分线上的点到角两边的距离相等可得DE=DF,利用HL易证Rt△BDE≌Rt△CDF,从而得到∠B=∠C,然后再用AAS证明△ABD≌△ACD即可得证.
(2)由∠BAC=60°和AB=AC可得△ABC为等边三角形,从而得到AB=BC=6,再由勾股定理求出高AD,即可求△ABC的面积.
(1)∵AD平分∠BAC,DE⊥AB,DF⊥AC
∴DE=DF,∠BAD=∠CAD
在Rt△BDE和Rt△CDF中,
∵BD=CD,DE=DF
∴Rt△BDE≌Rt△CDF(HL)
∴∠B=∠C
在△ABD和△ACD中,
∵∠BAD=∠CAD,∠B=∠C,BD=CD
∴△ABD≌△ACD(AAS)
∴AB=AC
(2)∵∠BAC=60°,AB=AC
∴△ABC为等边三角形
∴AB=BC=6
又∵△ABD≌△ACD(已证)
∴∠ADB=∠ADC=90°
∵BC=6,BD=CD
∴BD=3
在Rt△ABD中,AD=![]()
∴S△ABC=![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目