题目内容
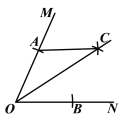
【题目】如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
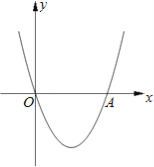
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.
【答案】解:(1)∵函数的图象与x轴相交于O,∴0=k+1,∴k=﹣1。
∴这个二次函数的解析式为y=x2﹣3x。
(2)如图,过点B做BD⊥x轴于点D,
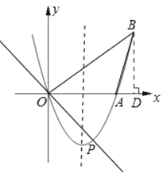
令x2﹣3x=0,解得:x=0或3。∴AO=3。
∵△AOB的面积等于6,∴![]() AOBD=6。∴BD=4。
AOBD=6。∴BD=4。
∵点B在函数y=x2﹣3x的图象上,
∴4=x2﹣3x,解得:x=4或x=﹣1(舍去)。
又∵顶点坐标为:( 1.5,﹣2.25),且2.25<4,
∴x轴下方不存在B点。
∴点B的坐标为:(4,4)。
(3)存在。
∵点B的坐标为:(4,4),∴∠BOD=45°,![]() 。
。
若∠POB=90°,则∠POD=45°。
设P点坐标为(x,x2﹣3x)。
∴![]() 。
。
若![]() ,解得x=4 或x=0(舍去)。此时不存在点P(与点B重合)。
,解得x=4 或x=0(舍去)。此时不存在点P(与点B重合)。
若![]() ,解得x=2 或x=0(舍去)。
,解得x=2 或x=0(舍去)。
当x=2时,x2﹣3x=﹣2。
∴点P 的坐标为(2,﹣2)。
∴![]() 。
。
∵∠POB=90°,∴△POB的面积为:![]() POBO=
POBO=![]() ×
×![]() ×
×![]() =8。
=8。
【解析】(1)将原点坐标代入抛物线中即可求出k的值,从而求得抛物线的解析式。
(2)根据(1)得出的抛物线的解析式可得出A点的坐标,也就求出了OA的长,根据△OAB的面积可求出B点纵坐标的绝对值,然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标,然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可。
(3)根据B点坐标可求出直线OB的解析式,由于OB⊥OP,由此可求出P点的坐标特点,代入二次函数解析式可得出P点的坐标.求△POB的面积时,求出OB,OP的长度即可求出△BOP的面积。

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案