Question

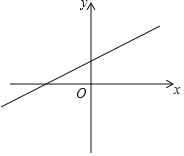
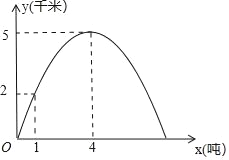
【题目】根据对宁波市相关的市场物价调研，某批发市场内甲种水果的销售利润y1（千元）与进货量x（吨）近似满足函数关系y1=0.25x，乙种水果的销售利润y2（千元）与进货量x（吨）之间的函数y2=ax2+bx+c的图象如图所示．

（1）求出y2与x之间的函数关系式；

（2）如果该市场准备进甲、乙两种水果共8吨，设乙水果的进货量为t吨，写出这两种水果所获得的销售利润之和W（千元）与t（吨）之间的函数关系式，并求出这两种水果各进多少吨时获得的销售利润之和最大，最大利润是多少？

Answer 1

【答案】（1）y2=﹣x2+x；（2）w=﹣（t﹣4）2+6，t=4时，w的值最大，最大值为6，

∴两种水果各进4吨时获得的销售利润之和最大，最大利润是6千元．

【解析】

（1）利用待定系数法即可解决问题；

（2）销售利润之和W=甲种水果的利润+乙种水果的利润，利用配方法求得二次函数的最值即可．

（1）∵函数y2=ax2+bx+c的图象经过（0，0），（1，2），（4，5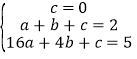），∴，解得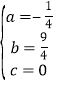：，∴y2=﹣x2+x．

（2）w = y1+y2=（8﹣t）﹣t2+t=﹣（t﹣4）2+6，∴t=4时，w的值最大，最大值为6，∴两种水果各进4吨时获得的销售利润之和最大，最大利润是6千元．