题目内容
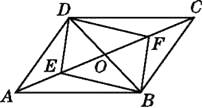
【题目】如图,在ABCD中,对角线AC,BD相交于O,E,F是对角线上的两点,给出下列四个条件:①OE=OF;
②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个
B.1个
C.2个
D.3个
【答案】B
【解析】解:①∵ABCD,∴OB=OD
∵OE=OF
∴四边形DEBF是平行四边形,因此①不符合题意;
②DE=BF不能判断四边形DEBF是平行四边形,因此②符合题意;
③∵ABCD,
∴AD=BC,AD∥BC
∴∠DAE=∠BCF
在△ADE和△BCF中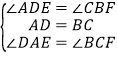
∴△ADE≌△BCF
∴DE=BF,∠DEA=∠BFC
∴∠DEA+∠DEO=180°,∠BFC+∠OFB=180°
∴∠DEO=∠OFB
∴DE∥BF DE=BF
∴四边形DEBF是平行四边形,因此③不符合题意;
④当∠ABE=∠CDF,与③的证明方法一样,可证出四边形DEBF是平行四边形,因此④不符合题意;
因此不能判定四边形DEBF是平行四边形只有②。
故答案为:B
利用平行四边形的性质及判断和全等三角形的性质及判断,逐一判断即可得出答案。

练习册系列答案
相关题目