Question

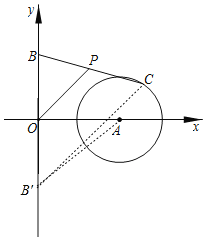
【题目】如图，在直角坐标系中，⊙A的半径为2，圆心坐标为（4，0），y轴上有点B（0，3），点C是⊙A上的动点，点P是BC的中点，则OP的范围是（　　）

A.B.2≤OP≤4C.≤OP≤D.3≤OP≤4

Answer 1

【答案】A

【解析】

如图，在y轴上取点B'（0，﹣3），连接B'C，B'A，由勾股定理可求B'A＝5，由三角形中位线定理可求B'C＝2OP，当点C在线段B'A上时，B'C的长度最小值＝5﹣2＝3，当点C在线段B'A的延长线上时，B'C的长度最大值＝5+2＝7，即可求解．

解：如图，在y轴上取点B'（0，﹣3），连接B'C，B'A，

∵点B（0，3），B'（0，﹣3），点A（4，0），

∴OB＝OB'＝3，OA＝4，

∴，

∵点P是BC的中点，

∴BP＝PC，

∵OB＝OB'，BP＝PC，

∴B'C＝2OP，

当点C在线段B'A上时，B'C的长度最小值＝5﹣2＝3，

当点C在线段B'A的延长线上时，B'C的长度最大值＝5+2＝7，

∴，

故选：A．