题目内容
【题目】因为一次函数y=kx+b与y=-kx+b(k≠0)的图象关于y轴对称,所以我们定义:函数y=kx+b与y=-kx+b(k≠0)互为“镜子”函数.
(1)请直接写出函数y=3x-2的“镜子”函数:______________;
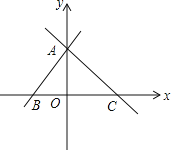
(2)如果一对“镜子”函数y=kx+b与y=-kx+b(k≠0)的图象交于点A,且与x轴交于B、C两点,如图所示,若△ABC是等腰直角三角形,∠BAC=90°,且它的面积是16,求这对“镜子”函数的解析式.
【答案】(1)y=-3x-2;(2)y=-x+4与y=x+4
【解析】
(1)直接利用“镜子”函数的定义得出答案;
(2)利用等腰直角三角形的性质得出AO=BO=CO,进而得出各点坐标,即可得出函数解析式.
(1)根据题意可得:函数y=3x-2的“镜子”函数:y=-3x-2;
故答案为:y=-3x-2;
(2)∵△ABC是等腰直角三角形,AO⊥BC,
∴AO=BO=CO,
∴设AO=BO=CO=x,根据题意可得:![]() x×2x=16,
x×2x=16,
解得:x=4,
则B(-4,0),C(4,0),A(0,4),
将B,A分别代入y=kx+b得:
![]() ,
,
解得:![]() ,
,
故其函数解析式为:y=x+4,
故其“镜子”函数为:y=-x+4.

练习册系列答案
相关题目
【题目】某种水果的价格如表:
购买的质量(千克) | 不超过10千克 | 超过10千克 |
每千克价格 | 6元 | 5元 |
张欣两次共购买了25千克这种水果(第二次多于第一次),共付款132元.问张欣第一次、第二次分别购买了多少千克这种水果?