题目内容
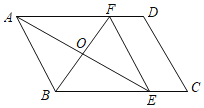
【题目】如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为( )

A. α B. ![]() C. 90﹣α D. 90﹣
C. 90﹣α D. 90﹣![]()
【答案】C
【解析】分析:过C作CE⊥AB于E,CF⊥BD于F,CG⊥AD于G,根据BC平分∠DBE,AC平分∠BAD,即可得到CD平分∠BDG,再根据三角形外角性质即可得出∠BDC的度数.
详解:如图, 过C作CE⊥AB于E,CF⊥BD于F,CG⊥AD于G,
∵∠ABD=52°,∠ABC=116°, ∴∠DBC=∠CBE=64°, ∴BC平分∠DBE, ∴CE=CF,
又∵AC平分∠BAD, ∴CE=CG, ∴CF=CG, 又∵CG⊥AD,CF⊥BD, ∴CD平分∠BDG,
∵∠CBE是△ABC的外角,∠DBE是△ABD的外角,
∴∠ABC=∠CBE-∠CAB=![]() ∠ADB, ∴∠ADB=2∠ACB=2α, ∴∠BDG=180°-2α,
∠ADB, ∴∠ADB=2∠ACB=2α, ∴∠BDG=180°-2α,
∴∠BDC=![]() ∠BDG=90°-α, 故选C.
∠BDG=90°-α, 故选C.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目