题目内容
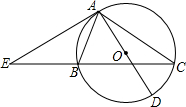
如图，△ABC内接于⊙O，AD是⊙O直径，过点A的切线与CB的延长线交于点E．
（1）求证：EA2=EB•EC；
（2）若EA=AC，cos∠EAB=
，AE=12，求⊙O的半径．
（1）求证：EA2=EB•EC；
（2）若EA=AC，cos∠EAB=
| 4 |
| 5 |
（1）证明：∵AE是切线，
∴∠EAB=∠C，
∵∠E是公共角，
∴△BAE∽△ACE，
∴EA：EC=EB：EA，
∴EA2=EB•EC；
（2）连接BD，过点B作BH⊥AE于点H，
∵EA=AC，
∴∠E=∠C，
∵∠EAB=∠C，
∴∠EAB=∠E，
∴AB=EB，
∴AH=EH=
AE=
×12=6，
∵cos∠EAB=
，
∴cos∠E=
，
∴在Rt△BEH中，BE=
=
，
∴AB=
，
∵AD是直径，
∴∠ABD=90°，
∵∠D=∠C，
∴cos∠D=
，
∴sin∠D=
，
∴AD=
=
，
∴⊙O的半径为
．
∴∠EAB=∠C，
∵∠E是公共角，
∴△BAE∽△ACE，
∴EA：EC=EB：EA，
∴EA2=EB•EC；
（2）连接BD，过点B作BH⊥AE于点H，∵EA=AC，
∴∠E=∠C，
∵∠EAB=∠C，
∴∠EAB=∠E，
∴AB=EB，
∴AH=EH=
| 1 |
| 2 |
| 1 |
| 2 |
∵cos∠EAB=
| 4 |
| 5 |
∴cos∠E=
| 4 |
| 5 |
∴在Rt△BEH中，BE=
| EH |
| cos∠E |
| 15 |
| 2 |
∴AB=
| 15 |
| 2 |
∵AD是直径，
∴∠ABD=90°，
∵∠D=∠C，
∴cos∠D=
| 4 |
| 5 |
∴sin∠D=
| 3 |
| 5 |
∴AD=
| AB |
| sin∠D |
| 25 |
| 2 |
∴⊙O的半径为
| 25 |
| 4 |
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
