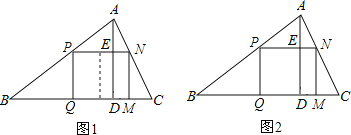题目内容
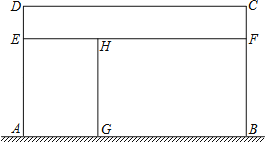
【题目】某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
【答案】(1)y=﹣![]() x2+55x,自变量x的取值范围为:24≤x<40;(2)当x=24时,y有最大值,最大值为528平方米.
x2+55x,自变量x的取值范围为:24≤x<40;(2)当x=24时,y有最大值,最大值为528平方米.
【解析】
试题分析:(1)根据矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,得到矩形AEFB面积是矩形CDEF面积的3倍,求得AD=3DE,于是得到y=x(55﹣![]() x)=﹣
x)=﹣![]() x2+55x,自变量x的取值范围为:24≤x<40;
x2+55x,自变量x的取值范围为:24≤x<40;
(2)把y=﹣![]() x2+55x化为顶点式:y=﹣
x2+55x化为顶点式:y=﹣![]() ( x﹣20)2+550,根据二次函数的性质即可得到结论.
( x﹣20)2+550,根据二次函数的性质即可得到结论.
解:(1)∵矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,
∴矩形AEFB面积是矩形CDEF面积的3倍,
∴AD=3DE,
∵AD=x,
∴GH=![]() x,
x,
∵围栏总长为110m,
∴2x+![]() x+2CD=110,
x+2CD=110,
∴CD=55﹣![]() x,
x,
∴y=x(55﹣![]() x)=﹣
x)=﹣![]() x2+55x,
x2+55x,
∴自变量x的取值范围为:24≤x<40;
(2)∵y=﹣![]() x2+55x=﹣
x2+55x=﹣![]() ( x2﹣40 x)=﹣
( x2﹣40 x)=﹣![]() ( x﹣20)2+550,
( x﹣20)2+550,
∵自变量x的取值范围为:24≤x<40,且二次项系数为﹣![]() <0,
<0,
∴当x=24时,y有最大值,最大值为528平方米.

【题目】在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y1 | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
y2 | … | 0 | 2 | 4 | 6 | 8 | 10 | 12 | … |
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为 ;
(2)当y1>y2时,自变量x的取值范围是 ;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.