Question

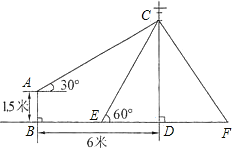
【题目】如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长（结果保留根号）．

Answer 1

【答案】（4+）米．

【解析】

试题分析：由题意可先过点A作AH⊥CD于H．在Rt△ACH中，可求出CH，进而CD=CH+HD=CH+AB，再在Rt△CED中，求出CE的长．

解：过点A作AH⊥CD，垂足为H，

由题意可知四边形ABDH为矩形，∠CAH=30°，

∴AB=DH=1.5，BD=AH=6，

在Rt△ACH中，tan∠CAH=，

∴CH=AHtan∠CAH，

∴CH=AHtan∠CAH=6tan30°=6×（米），

∵DH=1.5，∴CD=2+1.5，

在Rt△CDE中，

∵∠CED=60°，sin∠CED=，

∴CE==（4+）（米），

答：拉线CE的长为（4+）米．