��Ŀ����
����Ŀ����һ������������ABC�����ı�BC=120mm����AD=80mm����Ҫ�����ӹ��ɾ��������ʹ���ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ�
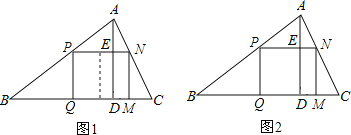
��1������˾��οɷָ���������ŷ��õ������Σ���ͼ1����ʱ�������������������ڱ߳��ֱ�Ϊ����mm��������㣮
��2�����������Ҫ�ӹ������ֻ�Ǿ��Σ���ͼ2���������˾�������������ڱ߳��Ͳ���ȷ���������������������ֵ����ﵽ������ֵʱ��������������ڱ߳���
���𰸡���1�������������������߳��ֱ�Ϊ![]() mm��
mm��![]() mm����2��S�����ֵΪ2400mm2����ʱPN=60mm��PQ=80��
mm����2��S�����ֵΪ2400mm2����ʱPN=60mm��PQ=80��![]() ��60=40��mm����
��60=40��mm����
��������
�����������1�����ھ��������������ŷ��õ�����������ɣ������PQ=ymm����PN=2ymm����֤��APN�ס�ABC�������������ε����ʽ�ɣ�
��2����PN=x����PQ��ʾ��AE�ij��ȣ�Ȼ��������������ζ�Ӧ�ߵıȵ������Ʊ��г�����ʽ����x��ʾ��PN��Ȼ����ݾ��ε������ʽ��ʽ���㣬�ٸ��ݶ��κ�������ֵ������
�⣺��1������εı߳�PN=2ymm����PQ=ymm��
��PN��BC��
���APN�ס�ABC��
��![]() ��
��
��![]() ��
��
���y=![]() ��
��
��PN=![]() ��2=
��2=![]() ��mm����
��mm����
�������������������߳��ֱ�Ϊ![]() mm��
mm��![]() mm��
mm��
��2����PN=xmm���������ɵ���APN�ס�ABC��
��![]() ��
��
��![]() ��
��
���PQ=80��![]() x��
x��
��S=PNPQ=x��80��![]() x��=��
x��=��![]() x2+80x=��
x2+80x=��![]() ��x��60��2+2400��
��x��60��2+2400��
��S�����ֵΪ2400mm2����ʱPN=60mm��PQ=80��![]() ��60=40��mm����
��60=40��mm����