��Ŀ����
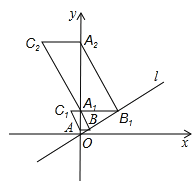
����Ŀ����ͼ����ƽ��ֱ�������У�ֱ��l����ԭ�㣬����y�����������е����Ϊ60�㣬����A��0��1����y��Ĵ��߽�ֱ��l�ڵ�B������B��ֱ��l�Ĵ��߽�y���ڵ�A1����A1B��BAΪ�ڱ�����ABA1C1������A1��y��Ĵ��߽�ֱ��l�ڵ�B1������B1��ֱ��l�Ĵ��߽�y���ڵ�A2����A2B1��B1A1Ϊ�ڱ�����A1B1A2C2������������������ȥ����Cn�����꣨ ��
A������![]() ��4n��4n�� B������
��4n��4n�� B������![]() ��4n��1��4n��1��
��4n��1��4n��1��
C������![]() ��4n��1��4n�� D������
��4n��1��4n�� D������![]() ��4n��4n��1��
��4n��4n��1��
���𰸡�C��
��������
�����������ֱ��l����ԭ�㣬����y�����������е����Ϊ60����
��ֱ��l�Ľ���ʽΪy=![]() x��
x��
��AB��y�ᣬ��A��0��1����
������B��������x��1����
��B��x��1������y=![]() x����1=
x����1=![]() x�����x=
x�����x=![]() ��
��
��B��������![]() ��1����AB=
��1����AB=![]() ��
��
��Rt��A1AB����AA1B=90��-60��=30������A1AB=90����
��AA1=![]() AB=3��OA1=OA+AA1=1+3=4��
AB=3��OA1=OA+AA1=1+3=4��
��ABA1C1��A1C1=AB=![]() ��
��
��C1���������-![]() ��4��������-
��4��������-![]() ��40��41����
��40��41����
��![]() x=4�����x=4
x=4�����x=4![]() ��
��
��B1��������4![]() ��4����A1B1=4
��4����A1B1=4![]() ��
��
��Rt��A2A1B1����A1A2B1=30������A2A1B1=90����
��A1A2=![]() A1B1=12��OA2=OA1+A1A2=4+12=16��
A1B1=12��OA2=OA1+A1A2=4+12=16��
��A1B1A2C2��A2C2=A1B1=4![]() ��
��
��C2���������-4![]() ��16��������-
��16��������-![]() ��41��42����
��41��42����
ͬ�����ɵ�C3�������Ϊ��-16![]() ��4��������-
��4��������-![]() ��42��43����
��42��43����
�Դ����ƣ���Cn�������ǣ�-![]() ��4n-1��4n����
��4n-1��4n����
��ѡC��