题目内容
【题目】已知:如图,矩形ABCD的对角线相交于点O,
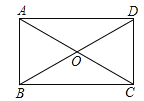
(1)若AB=2,∠AOD=120,求对角线AC的长;
(2)若AC=2AB.求证:△AOB是等边三角形.
【答案】(1)4;(2)证明见解析.
【解析】
试题分析:(1)根据矩形的对角线互相平分且相等可得OA=OB=![]() AC,根据邻补角的定义求出∠AOB,然后判断出△AOB是等边三角形,根据等边三角形的性质可得OA=AB,然后求解即可;
AC,根据邻补角的定义求出∠AOB,然后判断出△AOB是等边三角形,根据等边三角形的性质可得OA=AB,然后求解即可;
(2)由矩形的性质易得:AC=2AO=2BO,又因为AC=2AB,所以AO=BO=AB,进而可证明△AOB是等边三角形.
试题解析:(1)∵矩形ABCD的两条对角线交于点O,
∴OA=OB=![]() AC,
AC,
∵∠AOD=120°,
∴∠AOB=180°-∠AOD=180°-120°=60°,
∴△AOB是等边三角形,
∴OA=AB=2,
∴AC=2OA=2×2=4;
(2)∵四边形ABCD是矩形,
∴AC=BD,AO=CO=![]() AC,BO=DO=
AC,BO=DO=![]() BD,
BD,
∴AO=BO=![]() AC,
AC,
∵AC=2AB,
∴AO=BO=AB,
∴△AOB是等边三角形.

练习册系列答案
相关题目