题目内容
【题目】如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为 ![]() ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 . 
【答案】![]() +
+ ![]() ﹣
﹣ ![]()
【解析】解:连接CD′和BC′, ∵∠DAB=60°,
∴∠DAC=∠CAB=30°,
∵∠C′AB′=30°,
∴A、D′、C及A、B、C′分别共线.
∴AC= ![]()
∴扇形ACC′的面积为: ![]() =
= ![]() ,
,
∵AC=AC′,AD′=AB
∴在△OCD′和△OC'B中, 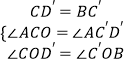
∴△OCD′≌△OC′B(AAS).
∴OB=OD′,CO=C′O
∵∠CBC′=60°,∠BC′O=30°
∴∠COD′=90°
∵CD′=AC﹣AD′= ![]() ﹣1
﹣1
OB+C′O=1
∴在Rt△BOC′中,BO2+(1﹣BO)2=( ![]() ﹣1)2
﹣1)2
解得BO= ![]() ,C′O=
,C′O= ![]() ﹣
﹣ ![]() ,
,
∴S△OC′B= ![]() BOC′O=
BOC′O= ![]() ﹣
﹣ ![]()
∴图中阴影部分的面积为:S扇形ACC′﹣2S△OC′B= ![]() +
+ ![]() ﹣
﹣ ![]() .
.
故答案为: ![]() +
+ ![]() ﹣
﹣ ![]() .
.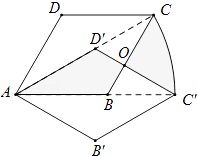
根据菱形的性质以及旋转角为30°,连接CD′和BC′,可得A、D′、C及A、B、C′分别共线,求出扇形面积,再根据AAS证得两个小三角形全等,求得其面积,最后根据扇形ACC′的面积﹣两个小的三角形面积即可.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目