题目内容
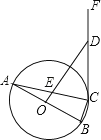
【题目】如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
①根据内错角相等,判定两直线平行;②根据两直线平行,同旁内角互补与同旁内角互补,两直线平行进行判定;③根据两直线平行,同旁内角互补与同角的补角相等判定;④∠D与∠ACB不能构成三线八角,无法判断.
∵∠1=∠2,
∴AB∥CD(内错角相等,两直线平行)
所以①正确;
∵AB∥CD(已证)
∴∠BAD+∠ADC=180°(两直线平行,同旁内角互补)
又∵∠BAD=∠BCD,
∴∠BCD+∠ADC=180°,
∴AD∥BC(同旁内角互补,两直线平行)
故②也正确;
∵AB∥CD,AD∥BC(已证)
∴∠B+∠BCD=180°,
∠D+∠BCD=180°,
∴∠B=∠D(同角的补角相等)
所以③也正确;
正确的有3个.
故选:C.

练习册系列答案
相关题目