Question

【题目】在△ABC中，AB＝AC，点D是直线BC上一点（不与B，C重合），以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连结CE．

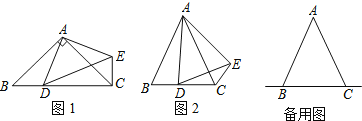
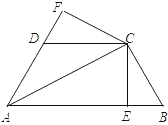
（1）如图1，当点D在线段BC上时，如果∠BAC＝90°，则∠BCE＝　 　°．

（2）设∠BAC＝α，∠BCE＝β．

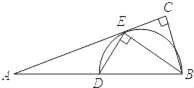
①如图2，当点D在线段BC上移动时，α，β之间有怎样的数量关系？请说明理由．

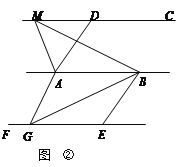
②当点D在直线BC上移动时，α，β之间有怎样的数量关系？请你在备用图上画出图形，并直接写出你的结论．

Answer 1

【答案】（1）90°；（2）①α+β＝180°，见解析；②见解析，α＝β

【解析】

（1）先用等式的性质得出∠CAE＝∠BAD，进而得出△ABD≌△ACE，有∠B＝∠ACE，最后用等式的性质即可得出结论；

（2）①由（1）的结论即可得出α+β＝180°；②同（1）的方法即可得出结论．

解：（1）∵∠DAE＝∠BAC，∠BAC＝∠BAD+∠DAC＝∠EAC+∠DAC；

∴∠CAE＝∠BAD；

在△ABD和△ACE中，

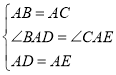
∴△ABD≌△ACE（SAS）；

∴∠B＝∠ACE；

∴∠BCE＝∠BCA+∠ACE＝∠BCA+∠B＝180°﹣∠BAC＝90°；

故答案为90°；

（2）①由（1）中可知β＝180°﹣α，

∴α、β存在的数量关系为α+β＝180°；

②当点D在射线BC上时，如图1，

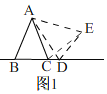
同（1）的方法即可得出，△ABD≌△ACE（SAS）；

∴∠ABD＝∠ACE，

∴β＝∠BCE＝∠ACB+∠ACE＝∠ACB+∠ABD＝180°﹣∠BAC＝180°﹣α，

∴α+β＝180°；

当点D在射线BC的反向延长线上时，如图2，

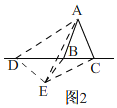
同（1）的方法即可得出，△ABD≌△ACE（SAS）；

∴∠ABD＝∠ACE，

∴β＝∠BCE＝∠ACE﹣∠ACB＝∠ABD﹣∠ACB＝∠BAC＝α，

∴α＝β．