题目内容
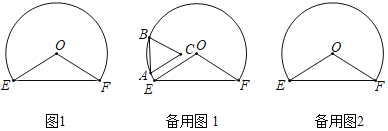
【题目】(1)如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值是_______.
的值是_______.
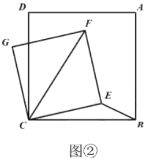
(2)如图②,在正方形![]() 中,
中,![]() ,点
,点![]() 是平面上一动点,且
是平面上一动点,且![]() ,连接
,连接![]() ,在
,在![]() 上方作正方形
上方作正方形![]() ,求线段
,求线段![]() 的最大值.
的最大值.
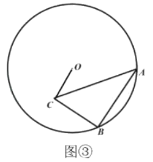
问题解决:(3)如图③,![]() 半径为6,在
半径为6,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 内,且
内,且![]() .当点
.当点![]() 在圆上运动时,求线段
在圆上运动时,求线段![]() 的最小值.
的最小值.
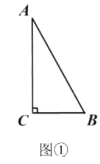
【答案】(1)![]() ;(2)
;(2)![]() ;(3)3
;(3)3
【解析】
(1)根据勾股定理算出AC,再根据正切的定义可得结果;
(2)根据题意得出当![]() 三点共线,且
三点共线,且![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值,即此时CF最大;
取得最大值,即此时CF最大;
(3)作![]() 的外接圆
的外接圆![]() ,连接
,连接![]() ,设
,设![]() 交劣弧
交劣弧![]() 于点
于点![]() ,则
,则![]() ,可得当点
,可得当点![]() 与点
与点![]() 重合时,线段
重合时,线段![]() 取得最小值,延长
取得最小值,延长![]() 交圆
交圆![]() 于点
于点![]() ,连接
,连接![]() ,证明
,证明![]() 得出
得出![]() ,从而可得
,从而可得![]() ,根据
,根据![]() ,在△ABF中,利用勾股定理列出方程,解得AC2,在△AOC中,求出OC即可.
,在△ABF中,利用勾股定理列出方程,解得AC2,在△AOC中,求出OC即可.
解:(1)∵![]() ,
,![]() ,
,![]() ,
,
∴AC=![]() ,
,
∴tanA=![]() ;
;
(2)![]() ,点
,点![]() 为定点,
为定点,
![]() 点
点![]() 在以
在以![]() 为圆心,
为圆心,![]() 长为半径的圆上运动.
长为半径的圆上运动.
![]() 当
当![]() 三点共线,且
三点共线,且![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值,
取得最大值,
![]() 在正方形
在正方形![]() 中,
中,![]() ,
,
![]() 最大=5+2=7,
最大=5+2=7,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() 线段
线段![]() 的最大值为
的最大值为![]() ;
;
(3)如图①,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 在
在![]() 中
中![]() ,且
,且![]() ,
,
![]() 的大小不变.
的大小不变.
又![]() 点
点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 内,且
内,且![]() 的半径为6,
的半径为6,
![]() 的大小,弦
的大小,弦![]() 的长均为定值.
的长均为定值.
作![]() 的外接圆
的外接圆![]() ,则点
,则点![]() 在劣弧
在劣弧![]() 上(不包括端点
上(不包括端点![]() ),
),

如图②,连接![]() ,设
,设![]() 交劣弧
交劣弧![]() 于点
于点![]() ,则
,则![]() ,且当点
,且当点![]() 与点
与点![]() 重合时,线段
重合时,线段![]() 取得最小值.
取得最小值.
延长![]() 交圆
交圆![]() 于点
于点![]() ,连接
,连接![]() ,
,
![]() ,
,
![]() 经过点
经过点![]() ,
,
![]() ,点
,点![]() 在
在![]() 上,
上,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() 在
在![]() 中,
中,![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() 线段
线段![]() 的最小值是3.
的最小值是3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
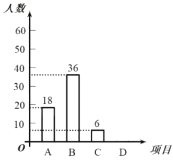
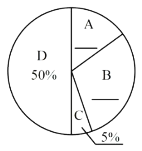
小学生10分钟应用题系列答案【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图
等级 | 成绩(得分) | 频数(人数) | 频率 |
A | 9~10分 | x | m |
B | 8~7 | 23 | 0.46 |
C | 6~5 | y | n |
D | 5分以下 | 3 | 0.06 |
(1)试直接写出x,y,m,n的值;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生400名,试估计这400名男生中成绩达到A等和B等的人数共有多少人?

【题目】二次函数y=ax2+bx+c(a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
给出以下结论:(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;(2)当﹣![]() <x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
<x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
A.0B.1C.2D.3