��Ŀ����
����Ŀ��̽��Ӧ��
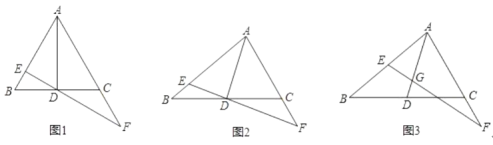
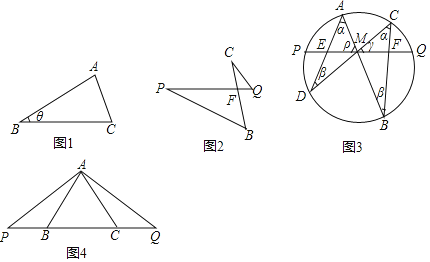
����һ����ͼ1������ABC�У�AB��c��BC��a����B��������c������ʾBC���ϵĸ�Ϊ�� ������a��c������ʾ��ABC�����Ϊ�� ����
���϶�����ͼ2����֪��C����P����֤��CFBF��QFPF��
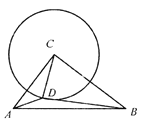
������������������ButterflyTheorem���ǹŴ�ŷ��ƽ�漸������ʵĽ��֮һ�����������1815�꣬��W��G���������֤����������ͼ����һֻ������
��������ͼ3��MΪ��PQ���е㣬��M����AB��CD������AD��BC��PQ�ֱ��ڵ�E��F����ME��MF��
֤��������A����C��������B����D������
��DMP����CMQ��������AMP����BMQ������
PM��MQ��a��ME��x��MF��y
��![]()
��![]()
����ã�MF2AEED��ME2CFFB
����![]() ,
,
����CFFB��QFFP��AEED��PEEQ��
��![]() ����
����![]()
��![]() ���Ӷ�x��y��ME��MF��
���Ӷ�x��y��ME��MF��
�����ú���������֤�����������������⣺
��ͼ4��B��CΪ�߶�PQ�ϵ����㣬��BP��CQ��AΪPQ��һ���㣬��������BAP����CAQ���ж���PAQ����״����֤����Ľ��ۣ�
���𰸡�����һ��![]() �����϶���֤��������������������PAQ����״Ϊ���������Σ�֤����������
�����϶���֤��������������������PAQ����״Ϊ���������Σ�֤����������
��������
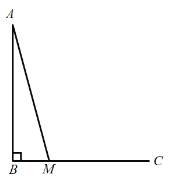
����һ����AD��BC��D�������Ǻ��������AD��AB��sinB��csin�����������������ʽ����ABC�������![]() BC��AD��
BC��AD��![]() acsin�����ɣ�
acsin�����ɣ�
���϶���֤����CFQ�ס�PFB���ó�![]() ��
��![]() �����ɵó����ۣ�
�����ɵó����ۣ�
��������֤S��ABP��S��ACQ��S��APC��S��AQB��֤��ABP�ס�ACQ����S��ABP��S��ACQ��֤��AP��AQ�����ɵó����ۣ�
����һ��
�⣺��AD��BC��D����ͼ1��ʾ��
��sinB��![]() ��
��
��AD��AB��sinB��csin����
���ABC�������![]() BC��AD��
BC��AD��![]() acsin����
acsin����
�ʴ�Ϊ��csin����![]() acsin����
acsin����
���϶���
֤�����ߡ�C����P����CFQ����PFB��
���CFQ�ס�PFB��
��![]() ��
��![]() ,
,
��CFBF��QFPF��
��������
�⣺��PAQ����״Ϊ���������Σ��������£�
��B��CΪ�߶�PQ�ϵ����㣬��BP��CQ��
��CP��BQ��
���ABP����ACQ�ȵȸߣ���APC����AQB�ȵȸߣ�
��S��ABP��S��ACQ��S��APC��S��AQB��
�ߡ�BAP����CAQ��
���BAP+��BAC����CAQ+��BAC��
����PAC����QAB��
��sin��QAB��Psin��PAC��
��S��AQB��![]() ABAQsin��QAB��S��APC��
ABAQsin��QAB��S��APC��![]() ACAPsin��PAC��
ACAPsin��PAC��
�� =
=![]() =1,
=1,
��![]() =
=![]() ��
��
���ABP�ס�ACQ��
��S��ABP��S��ACQ��
��![]() =
=![]() ��1��
��1��
��AP��AQ��
���PAQ����״Ϊ���������Σ�

 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�����Ŀ��2020���¹ڷ������鷢�����������й����ְ��Ա���������������߹������������������Ӯ����������ս.���У�A������500����ְ��Ա��Ϊ�˽Ȿ����2����3���ڼ���ְ��Ա�μ�Ӧ��ִ�ڵ������A�������ִ�ڵĴ��������ȡ50����ְ��Ա���е��飬�������ݽ����������������ͷ�������������˲�����Ϣ��
����x/�� | Ƶ�� | Ƶ�� |
0 ��x< 10 | 8 | 0.16 |
10��x< 20 | 10 | 0.20 |
20��x< 30 | 16 | b |
30��x< 40 | a | 0.24 |
x�� 40 | 4 | 0.08 |

���У�Ӧ��ִ�ڴ�����20��x< 30��һ��������ǣ�
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
�����������Ϣ������������⣺
��1��![]() =��������������
=��������������![]() =��������������
=��������������
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������ȡ��50����ְ��Ա�μ�Ӧ��ִ�ڴ�������λ������������������
��4�������2����3���ڼ�A������ְ��Ա�μ�Ӧ��ִ�ڵĴ���������30�ε�Լ��__�ˣ�