题目内容
【题目】在平面直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数为_________.
【答案】4
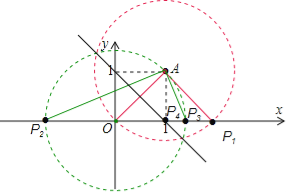
【解析】试题分析:本题应该分情况讨论.以OA为腰或底分别讨论.当A是顶角顶点时,P是以A为圆心,以OA为半径的圆与x轴的交点,共有1个,
当O是顶角顶点时,P是以O为圆心,以OA为半径的圆与x轴的交点,有2个;
P是OA的中垂线与x轴的交点,有1个,共有4个.
解:(1)若AO作为腰时,有两种情况,
当A是顶角顶点时,P是以A为圆心,以OA为半径的圆与x轴的交点,共有1个,
当O是顶角顶点时,P是以O为圆心,以OA为半径的圆与x轴的交点,有2个;
(2)若OA是底边时,P是OA的中垂线与x轴的交点,有1个.
以上4个交点没有重合的.故符合条件的点有4个.
故填:4.

练习册系列答案
相关题目
【题目】某种油菜籽在相同条件下发芽试验的结果如下:
每批粒数 | 100 | 400 | 800 | 1 000 | 2 000 | 4 000 |
发芽的频数 | 85 | 300 | 652 | 793 | 1 604 | 3204 |
发芽的频率 | 0.850 | 0.750 | 0.815 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计,该玉米种子发芽的概率为___(精确到0.1).